题目内容
 画出函数f(x)=
画出函数f(x)=
|
(1)填写下表:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||
| f(x)=x2+2x | |||||||||
f(x)=(
|
(3)f(x)的增区间是:
(-1,0)
(-1,0)
,减区间是:(-∞,-1)、(0,+∞)
(-∞,-1)、(0,+∞)
.分析:(1)根据函数的对应法则,结合指数的运算法则求出各个函数值,即可填写题中的表格;
(2)由二次函数的图象作法和指数函数的图象与性质,可得函数的图象是开口向上的抛物线y=x2+2x位于y轴左侧的部分,以及指数函数y=(
)x位于y轴右侧部分组合而成,因此可作函数的图象;
(3)由二次函数的图象与性质和指数函数的单调性,结合(2)中作出的图象即可得到函数的单调区间.
(2)由二次函数的图象作法和指数函数的图象与性质,可得函数的图象是开口向上的抛物线y=x2+2x位于y轴左侧的部分,以及指数函数y=(
| 1 |
| 2 |
(3)由二次函数的图象与性质和指数函数的单调性,结合(2)中作出的图象即可得到函数的单调区间.
解答:解:(1)根据函数的解析式,可得
(2)∵当x≤0时,f(x)=x2+2x是二次函数;当x>0时,f(x)=(
)x是指数函数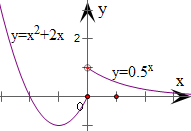
∴函数的图象是开口向上的抛物线y=x2+2x位于y轴左侧的部分,
以及指数函数y=(
)x位于y轴右侧部分组合而成,
因此作出函数的图象,如右图所示
(3)∵抛物线y=x2+2x开口向上,关于直线x=-1对称
∴函数f(x)在(-∞,-1)上是减函数,且在(-1,0)上是增函数
又∵y=(
)x的底数
∈(0,1),
∴函数f(x)在(0,+∞)上是减函数
因此,函数y=f(x)的增区间是(-1,0),减区间是(-∞,-1)、(0,+∞).
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | ||||||||
| f(x)=x2+2x | 3 | 0 | -1 | 0 | 3 | 8 | 15 | ||||||||
f(x)=(
|
8 | 4 | 2 | 1 |
|
|
|
| 1 |
| 2 |

∴函数的图象是开口向上的抛物线y=x2+2x位于y轴左侧的部分,
以及指数函数y=(
| 1 |
| 2 |
因此作出函数的图象,如右图所示
(3)∵抛物线y=x2+2x开口向上,关于直线x=-1对称
∴函数f(x)在(-∞,-1)上是减函数,且在(-1,0)上是增函数
又∵y=(
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)在(0,+∞)上是减函数
因此,函数y=f(x)的增区间是(-1,0),减区间是(-∞,-1)、(0,+∞).
点评:本题给出含有指数和二次函数的分段函数,求函数的值并作函数的图象,着重考查了基本初等函数的图象与性质、函数的单调性等知识,属于基础题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 在同一平面直角坐标系中,画出函数u(x)=3sinx-cosx,v(x)=sin(2x)+3cos(2x),φ(x)=2sinx+2cosx的部分图象如下,则( )
在同一平面直角坐标系中,画出函数u(x)=3sinx-cosx,v(x)=sin(2x)+3cos(2x),φ(x)=2sinx+2cosx的部分图象如下,则( )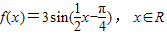 .
.