题目内容
已知α是第三象限的角,sinα=﹣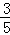 ,则
,则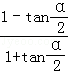 =( )
=( )
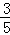 ,则
,则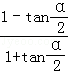 =( )
=( )A.﹣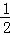 | B.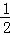 | C.2 | D.﹣2 |
D
∵α是第三象限角,
∴2kπ+π<α<2kπ+
∴kπ+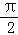 <
< <kπ+
<kπ+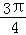
∴tan <﹣1
<﹣1
sinα= 整理得3tan2
整理得3tan2 +10tan
+10tan  +3=0
+3=0
求得tan =﹣3或﹣
=﹣3或﹣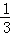 (排除)
(排除)
则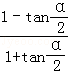 =﹣2
=﹣2
故选D.
∴2kπ+π<α<2kπ+

∴kπ+
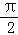 <
< <kπ+
<kπ+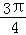
∴tan
 <﹣1
<﹣1sinα=
 整理得3tan2
整理得3tan2 +10tan
+10tan  +3=0
+3=0求得tan
 =﹣3或﹣
=﹣3或﹣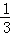 (排除)
(排除)则
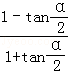 =﹣2
=﹣2故选D.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 均为锐角,且
均为锐角,且 ,
, .
.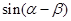 的值;(2)求
的值;(2)求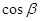 的值.
的值.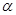 的终边与单位圆交于点P(
的终边与单位圆交于点P(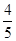 ,
,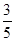 ).
).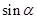 、
、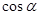 、
、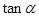 值;
值;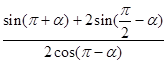 的值.
的值. 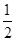 +cos α,且α∈
+cos α,且α∈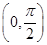 ,则
,则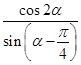 的值为________.
的值为________. 中,
中, ,
, ,则
,则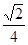



 ________.
________. ,则
,则 ______.
______. ( )
( )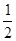

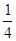
 =( )
=( )
