题目内容
将函数 向右平移
向右平移 个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与
个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与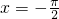 ,
, ,x轴围成的图形面积为
,x轴围成的图形面积为
- A.

- B.

- C.
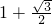
- D.
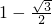
B
分析:将函数 向右平移
向右平移 个单位,推出函数解析式,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,利用积分求函数y=g(x)与
个单位,推出函数解析式,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,利用积分求函数y=g(x)与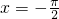 ,
, ,x轴围成的图形面积.
,x轴围成的图形面积.
解答:将函数 向右平移
向右平移 个单位,得到函数
个单位,得到函数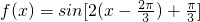 =sin(2x+π)=-sin2x,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)=-sinx的图象,则函数y=-sinx与
=sin(2x+π)=-sin2x,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)=-sinx的图象,则函数y=-sinx与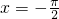 ,
, ,x轴围成的图形面积:-
,x轴围成的图形面积:- +
+ (-sinx)dx=-cosx
(-sinx)dx=-cosx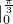 +cosx
+cosx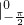 =
= +1=
+1=
故选B
点评:本题是中档题,考查三角函数图象的平移伸缩变换,利用积分求面积,正确的变换是基础,合理利用积分求面积是近年高考必考内容.
分析:将函数
 向右平移
向右平移 个单位,推出函数解析式,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,利用积分求函数y=g(x)与
个单位,推出函数解析式,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,利用积分求函数y=g(x)与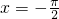 ,
, ,x轴围成的图形面积.
,x轴围成的图形面积.解答:将函数
 向右平移
向右平移 个单位,得到函数
个单位,得到函数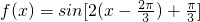 =sin(2x+π)=-sin2x,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)=-sinx的图象,则函数y=-sinx与
=sin(2x+π)=-sin2x,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)=-sinx的图象,则函数y=-sinx与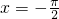 ,
, ,x轴围成的图形面积:-
,x轴围成的图形面积:- +
+ (-sinx)dx=-cosx
(-sinx)dx=-cosx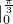 +cosx
+cosx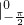 =
= +1=
+1=
故选B
点评:本题是中档题,考查三角函数图象的平移伸缩变换,利用积分求面积,正确的变换是基础,合理利用积分求面积是近年高考必考内容.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
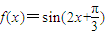 向右平移
向右平移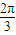 个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与
个单位,再将所得的函数图象上的各点纵坐标不变,横坐标变为原来的2倍,得到函数y=g(x)的图象,则函数y=g(x)与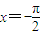 ,
,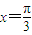 ,x轴围成的图形面积为( )
,x轴围成的图形面积为( )

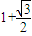
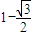
 )图像上各点的横坐标缩短为原来的
)图像上各点的横坐标缩短为原来的 倍(纵坐标不变),再将图像向右平移
倍(纵坐标不变),再将图像向右平移 个单位,那么所得图像的一条对称轴方程为
( )
个单位,那么所得图像的一条对称轴方程为
( ) B.x =-
B.x =- C.x =
C.x = D.x =
D.x = )图像上各点的横坐标缩短为原来的
)图像上各点的横坐标缩短为原来的 倍(纵坐标不变),再将图像向右平移
倍(纵坐标不变),再将图像向右平移 个单位,那么所得图像的一条对称轴方程为 ( )
个单位,那么所得图像的一条对称轴方程为 ( ) B. x=-
B. x=-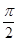 C.x =
C.x = D.x =
D.x =