题目内容
已知过A(0,1),B(1,2)的圆C的圆心在第一象限,且弧AB对的圆周角为
.
(1)求圆C的方程.
(2)若D(2,-1),求∠ADB的角平线的方程.
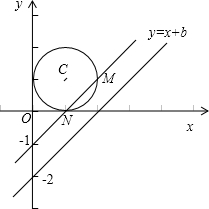
(3)若直线y=x+b,(-2≤b≤-1),求直线扫过圆的面积.
| π | 4 |
(1)求圆C的方程.
(2)若D(2,-1),求∠ADB的角平线的方程.
(3)若直线y=x+b,(-2≤b≤-1),求直线扫过圆的面积.
分析:(1)由题意可得圆C的圆心在第一象限且在线段AB的中垂线上,根据线段AB的中垂线方程设出圆心C 的坐标,再根据
AC⊥BC,斜率之积等于-1求出圆心C 的坐标,进而得到半径,由此求得圆C的方程.
(2)根据DB到∠ADB的角平线的角等于∠ADB的角平分线到DA的角,可得
=
,解得∠ADB的角平分线 k 的值,用点斜式求出∠ADB的角平线的方程.
(3)当b=-1时,求出截圆得到的弦长为 MN 的值,可得∠MCN=
.b=-2 时,直线和圆相离,直线扫过的面积是一个弓形,其面积等于扇形MCN的面积减去等腰直角三角形MCN的面积.
AC⊥BC,斜率之积等于-1求出圆心C 的坐标,进而得到半径,由此求得圆C的方程.
(2)根据DB到∠ADB的角平线的角等于∠ADB的角平分线到DA的角,可得
| k+3 |
| 1+k(-3) |
| -1-k |
| 1+(-1)k |
(3)当b=-1时,求出截圆得到的弦长为 MN 的值,可得∠MCN=
| π |
| 2 |
解答:解:(1)由题意可得圆C的圆心在第一象限且在线段AB的中垂线上,且弧AB对的圆心角为
.
又AB的中点M(
,
),AB的斜率等于
=1,故AB的中垂线方程为y-
=-1•(x-
),
即x+y-2=0.
故可设C(a,2-a),再由AC⊥BC可得
•
=-1,解得a=1,
故圆心C(1,1),半径等于|CA|=
=1,
故圆C的方程为(x-1)2+(y-1)2=1.
(2)设∠ADB的角平线的斜率等于k,由于DB的斜率k1=
=-3,DA的斜率k2=
=-1.
由题意可得DB到∠ADB的角平线的角等于∠ADB的角平分线到DA的角,
故有
=
,解得 k=
(舍去),k=
,
∴∠ADB的角平线的方程 y+1=
(x-2),即(
+1)x+2y-2
=0.
(3)当b=-1时,直线直线y=x+b 即x-y-1=0,圆心C到直线的距离等于
=
,
截圆得到的弦长为 MN=2
=
,故∠MCN=
.
b=-2 时,直线直线y=x-2 即x-y-2=0,圆心C到直线的距离等于
=
大于半径,
此时直线和圆相离.
直线扫过的面积是一个弓形,其面积等于扇形MCN的面积减去等腰直角三角形MCN的面积,
即
×π×12-
×1×1=
.
| π |
| 2 |
又AB的中点M(
| 1 |
| 2 |
| 3 |
| 2 |
| 2-1 |
| 1-0 |
| 3 |
| 2 |
| 1 |
| 2 |
即x+y-2=0.
故可设C(a,2-a),再由AC⊥BC可得
| 1-a-1 |
| a-0 |
| 1-a-2 |
| a-1 |
故圆心C(1,1),半径等于|CA|=
| 1+0 |
故圆C的方程为(x-1)2+(y-1)2=1.
(2)设∠ADB的角平线的斜率等于k,由于DB的斜率k1=
| 2+1 |
| 1-2 |
| 1+1 |
| 0-2 |
由题意可得DB到∠ADB的角平线的角等于∠ADB的角平分线到DA的角,
故有
| k+3 |
| 1+k(-3) |
| -1-k |
| 1+(-1)k |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∴∠ADB的角平线的方程 y+1=
-1-
| ||
| 2 |
| 5 |
| 5 |
(3)当b=-1时,直线直线y=x+b 即x-y-1=0,圆心C到直线的距离等于
| 1 | ||
|
| ||
| 2 |
截圆得到的弦长为 MN=2
1-
|
| 2 |
| π |
| 2 |
b=-2 时,直线直线y=x-2 即x-y-2=0,圆心C到直线的距离等于
| 2 | ||
|
| 2 |
此时直线和圆相离.
直线扫过的面积是一个弓形,其面积等于扇形MCN的面积减去等腰直角三角形MCN的面积,
即
| 1 |
| 4 |
| 1 |
| 2 |
| π-2 |
| 4 |

点评:本题主要考查求圆的标准方程的方法,直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.