题目内容
设 和
和 为双曲线
为双曲线 (
(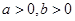 )的两个焦点, 若F1 、F2,
)的两个焦点, 若F1 、F2,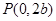 是正三角形的三个顶点,则双曲线的离心率为
是正三角形的三个顶点,则双曲线的离心率为
2.
解析试题分析:因为F1 、F2,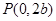 是正三角形的三个顶点,所以
是正三角形的三个顶点,所以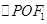 是直角三角形,由勾股定理得
是直角三角形,由勾股定理得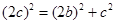 ,又
,又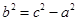 ,所以
,所以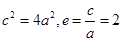 。
。
考点:本题主要考查双曲线的几何性质
点评:简单题,利用数形结合思想,集合正三角形的条件,建立a,b,c的 关系。

练习册系列答案
相关题目
题目内容
设 和
和 为双曲线
为双曲线 (
(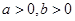 )的两个焦点, 若F1 、F2,
)的两个焦点, 若F1 、F2,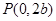 是正三角形的三个顶点,则双曲线的离心率为
是正三角形的三个顶点,则双曲线的离心率为
2.
解析试题分析:因为F1 、F2,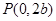 是正三角形的三个顶点,所以
是正三角形的三个顶点,所以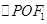 是直角三角形,由勾股定理得
是直角三角形,由勾股定理得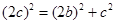 ,又
,又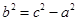 ,所以
,所以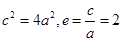 。
。
考点:本题主要考查双曲线的几何性质
点评:简单题,利用数形结合思想,集合正三角形的条件,建立a,b,c的 关系。
