题目内容
(理科)设四面体的四个面的面积分别为S1,S2,S3,S4,其中它们的最大值为S,则
的取值范围是( )
| S1+S2+S3+S4 |
| S |
分析:根据棱锥的结构特征,我们结合四面体的四个面的面积分别为S1,S2,S3,S4,其中它们的最大值为S,可得当S1=S2=S3=S4时,
取最大值4,当“棱锥的顶点落在底面上时”(极限思想)
取最小值2,进而得到答案.
| S1+S2+S3+S4 |
| S |
| S1+S2+S3+S4 |
| S |
解答:解:∵四面体的四个面的面积分别为S1,S2,S3,S4,
S表示它们的最大值
故当S1=S2=S3=S4时,
取最大值4
即
≤4
棱锥的高趋近0时,
S1+S2+S3+S4的值趋近2
∴S1+S2+S3+S4>2S
故
>2
故
的取值范围是(2,4]
故选B
S表示它们的最大值
故当S1=S2=S3=S4时,
| S1+S2+S3+S4 |
| S |
即
| S1+S2+S3+S4 |
| S |
棱锥的高趋近0时,
S1+S2+S3+S4的值趋近2
∴S1+S2+S3+S4>2S
故
| S1+S2+S3+S4 |
| S |
故
| S1+S2+S3+S4 |
| S |
故选B
点评:本题考查的知识点是棱锥的结构特征,其中根据已知条件和棱锥的结构特征,判断出
的最大值和下界是解答本题的关键.
| S1+S2+S3+S4 |
| S |

练习册系列答案
相关题目
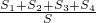 的取值范围是
的取值范围是 的取值范围是( )
的取值范围是( )