题目内容
已知向量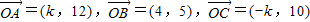
，且A、B、C三点共线，则k= ．
【答案】分析：利用三点共线得到以三点中的一点为起点，另两点为终点的两个向量平行，利用向量平行的坐标形式的充要条件列出方程求出k．
解答：解：向量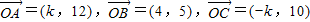
，
∴
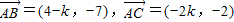
又A、B、C三点共线
故（4-k，-7）=λ（-2k，-2）
∴k=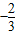
故答案为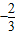
点评：本题考查向量平行的坐标形式的充要条件、向量平行解决三点共线．
解答：解：向量
，∴
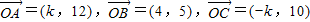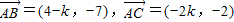
又A、B、C三点共线
故（4-k，-7）=λ（-2k，-2）
∴k=
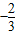
故答案为
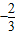
点评：本题考查向量平行的坐标形式的充要条件、向量平行解决三点共线．
练习册系列答案
相关题目
，且A、B、C分别为△ABC的三边a、b、c所对的角。
边的长。
，且A、B、C三点共线，
，且A、B、C分别为
的三边a、b、c所对的角。
求c边的长。
，且A，B，C分别是△ABC三边a，b，c所对的角．
，求c的值．
，且A，B，C分别是△ABC三边a，b，c所对的角．
，求c的值．