题目内容
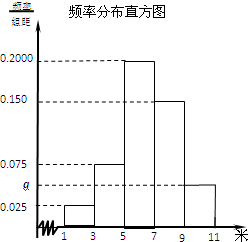 为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11)五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成[1,3),[3,5),[5,7),[7,9),[9,11)五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.(1)求实数a的值及参加“掷铅球”项目测试的人数;
(2)若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生自不同组的概率.
分析:(1)由频率分布直方图的性质可得:(0.2+0.15+0.075+a+0.025)×2=1,解得a即可;
(2)设从此次测试成绩最好和最差的两组中随机抽取2名学生自不同组的事件为A:由已知,测试成绩在[1,3)有2人,记为a,b;在[9,11]有4人,记为A,B,C,D. 从这6人中随机抽取2人有
即15种情况.其中事件A包括
×
即共8种情况. 再利用古典概型的概率计算公式即可得出.
(2)设从此次测试成绩最好和最差的两组中随机抽取2名学生自不同组的事件为A:由已知,测试成绩在[1,3)有2人,记为a,b;在[9,11]有4人,记为A,B,C,D. 从这6人中随机抽取2人有
| C | 2 6 |
| C | 1 2 |
| C | 1 4 |
解答:解:(1)由题意可知(0.2+0.15+0.075+a+0.025)×2=1,解得a=0.05.
∴此次测试总人数为
=40..
答:此次参加“掷铅球”的项目测试的人数为40人.
(2)设从此次测试成绩最好和最差的两组中随机抽取2名学生自不同组的事件为A:
由已知,测试成绩在[1,3)有2人,记为a,b;在[9,11]有4人,记为A,B,C,D.
从这6人中随机抽取2人有
即15种情况.
事件A包括
×
即共8种情况.
∴P(A)=
.
答:随机抽取的2名学生自不同组的概率为
.
∴此次测试总人数为
| 4 |
| 0.05×2 |
答:此次参加“掷铅球”的项目测试的人数为40人.
(2)设从此次测试成绩最好和最差的两组中随机抽取2名学生自不同组的事件为A:
由已知,测试成绩在[1,3)有2人,记为a,b;在[9,11]有4人,记为A,B,C,D.
从这6人中随机抽取2人有
| C | 2 6 |
事件A包括
| C | 1 2 |
| C | 1 4 |
∴P(A)=
| 8 |
| 15 |
答:随机抽取的2名学生自不同组的概率为
| 8 |
| 15 |
点评:本题考查了频率分布直方图的性质、古典概型的概率计算公式,属于中档题.

练习册系列答案
相关题目
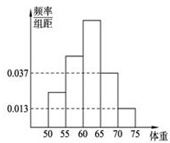 为了解某校今年准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12,则报考飞行员的总人数是
为了解某校今年准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12,则报考飞行员的总人数是 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数; 个小组的频率之比为
个小组的频率之比为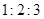 ,其中第
,其中第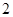 小组的频数为
小组的频数为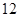 ,则报考飞行员的总人数是 .
,则报考飞行员的总人数是 .
