题目内容
若1>a>b>0,则下列式子成立的是(1)(
| 1 |
| 2 |
| 1 |
| 2 |
(4)loga2>logb2(5)aabb>abba.
分析:根据1>a>b>0,由不等式的基本性质结合指数函数,幂函数的性质对四个选项进行逐一判断即可.
解答:解:∵1>a>b>0,
(1)、考察指数函数y=(
) x,它在R上是减函数,∵b<a,∴(
)a<(
)b,
故本选项正确;
(2)、考察幂函数y=x5,它在R上是增函数,∵b<a,∴a5>b5,
故本选项正确;
(3)、考察a-b的范围:0<a-b<1故log2(a-b)<0,故本选项不正确;
(4)、考察指数函数y=logx2=
,它在(0,1)上是减函数,∵b<a,∴loga2<logb2,
故本选项不正确;
(5)、考察(
) a-b >(
) 0=1,得:aabb>abba,故本选项正确;
故答案为:(1)(2)(5).
(1)、考察指数函数y=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故本选项正确;
(2)、考察幂函数y=x5,它在R上是增函数,∵b<a,∴a5>b5,
故本选项正确;
(3)、考察a-b的范围:0<a-b<1故log2(a-b)<0,故本选项不正确;
(4)、考察指数函数y=logx2=
| 1 |
| log 2x |
故本选项不正确;
(5)、考察(
| a |
| b |
| a |
| b |
故答案为:(1)(2)(5).
点评:本题考查的是不等式的基本性质,熟知基本初等函数的基本性质是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
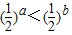 ; (2)a5>b5; (3)log2(a-b)>0;
; (2)a5>b5; (3)log2(a-b)>0;