题目内容
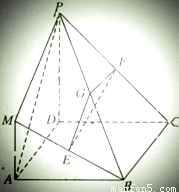
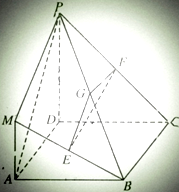 如,四边形ABCD是边长为a的正方形,PD⊥平面ABCD,MA∥PD,E,F,G分别为MB,PC,PB的中点,且AD=PD=2MA.
如,四边形ABCD是边长为a的正方形,PD⊥平面ABCD,MA∥PD,E,F,G分别为MB,PC,PB的中点,且AD=PD=2MA.(1)求证:平面EFG⊥平面PDC;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.
分析:(1)要证平面EFG⊥平面PDC,只需在平面EFG内找一直线与平面PDC垂直,而根据线面垂直的判定定理可知GF⊥平面PDC,GF∈平面EFG,满足定理条件,即可得证;(2)设MA=1,求出PD=AD,得到Vp-ABCD=
S正方形ABCD•PD,求出PD,根据DA⊥面MAB,可得DA即为点P到平面MAB的距离,根据三棱锥的体积公式求出体积得到V P-MAB:V P-ABCD的比值.
| 1 |
| 3 |
解答:(1)证明:由已知PD⊥平面ABCD,
因为BC∈平面ABCD,所以PD⊥BC,
因为四边形ABCD为正方形,所以BC⊥CD,
又PD∩DC=D,所以BC⊥平面PDC,
在△PBC中,因为G、F分别是PB、PC中点,
所以GF∥BC,故GF⊥平面PDC,又GF∈平面EFG,
所以平面EFG⊥平面PDC;
(2)因为PD⊥平面ABCD,
四边形ABCD为正方形,不妨设MA=1,
则PD=AD=2,所以Vp-ABCD=
S正方形ABCD•PD=
,
由于DA⊥面MAB,所以DA即为点P到平面MAB的距离,
所以三棱锥Vp-MAB=
×
×1×2×2=
,
所以V P-MAB:V P-ABCD=1:4.
因为BC∈平面ABCD,所以PD⊥BC,
因为四边形ABCD为正方形,所以BC⊥CD,
又PD∩DC=D,所以BC⊥平面PDC,
在△PBC中,因为G、F分别是PB、PC中点,
所以GF∥BC,故GF⊥平面PDC,又GF∈平面EFG,
所以平面EFG⊥平面PDC;
(2)因为PD⊥平面ABCD,
四边形ABCD为正方形,不妨设MA=1,
则PD=AD=2,所以Vp-ABCD=
| 1 |
| 3 |
| 8 |
| 3 |
由于DA⊥面MAB,所以DA即为点P到平面MAB的距离,
所以三棱锥Vp-MAB=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
所以V P-MAB:V P-ABCD=1:4.
点评:本题考查空间中的线面关系,考查线面垂直、面面垂直的判定及几何体体积的计算,考查试图能力和逻辑思维能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
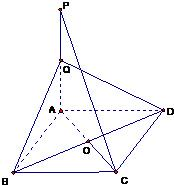
 15、如图四边形ABCD是菱形,PA⊥平面ABCD,Q为PA的中点.
15、如图四边形ABCD是菱形,PA⊥平面ABCD,Q为PA的中点.