题目内容
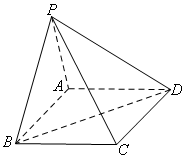
如图,在四棱锥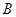 中,底面
中,底面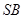 是直角梯形,
是直角梯形,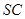 ∥
∥ ,
, ,
, ⊥平面SAD,点
⊥平面SAD,点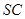 是
是 的中点,且
的中点,且 ,
, .
.
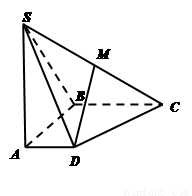
(1)求四棱锥 的体积;
的体积;
(2)求证: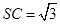 ∥平面
∥平面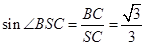 ;
;
(3)求直线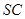 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
【答案】
(1)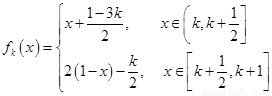 ;
;
(2)
取 的中点
的中点 ,连接
,连接 、
、 。
。 ∥
∥ 且
且

由底面 是直角梯形,
是直角梯形, 垂直于
垂直于 和
和 ,得到
,得到 ∥
∥ 且
且
 ,从而
,从而 ∥
∥ 且
且
 ,由 四边形
,由 四边形 是平行四边形推出
是平行四边形推出 ∥
∥ ,得到
,得到 ∥平面
∥平面 ;
;
(3)直线 和平面
和平面 所成的角的正弦值是
所成的角的正弦值是 。
。
【解析】
试题分析:(1)∵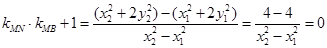 ⊥底面
⊥底面 ,
, 底面
底面 ,
, 底面
底面

∴ 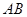 ⊥
⊥ ,
,  ⊥
⊥
∵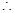 ,
, 、
、 是平面
是平面 内的两条相交直线
内的两条相交直线
∴ 侧棱 底面
底面 2分
2分
在四棱锥 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 是直角梯形,
是直角梯形,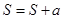 ∥
∥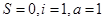 ,
,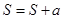 ⊥
⊥ ,
, ,
,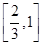
∴ 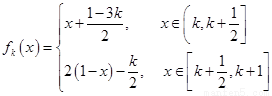 4分
4分
(2)
取 的中点
的中点 ,
,
连接 、
、 。
。
∵ 点 是
是 的中点
的中点
∴ ∥
∥ 且
且

∵ 底面 是直角梯形,
是直角梯形, 垂直于
垂直于 和
和 ,
, ,
,
∴  ∥
∥ 且
且

∴  ∥
∥ 且
且

∴ 四边形 是平行四边形
是平行四边形
∴  ∥
∥
∵ ,
,
∴  ∥平面
∥平面 8分
8分
(3)∵ 侧棱 底面
底面 ,
, 底面
底面
∴ 
∵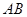 垂直于
垂直于 ,
,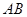 、
、 是平面
是平面 内的两条相交直线
内的两条相交直线
∴ 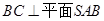 ,垂足是点
,垂足是点
∴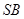 是
是 在平面
在平面 内的射影,
内的射影,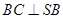
∴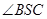 是直线
是直线 和平面
和平面 所成的角
所成的角
∵ 在 中,
中, ,
,
∴
∴
∴ 直线 和平面
和平面 所成的角的正弦值是
所成的角的正弦值是 13分
13分
考点:本题主要考查立体几何中的平行关系、垂直关系,角及体积计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用空间向量,能省去繁琐的证明,也是解决立体几何问题的一个基本思路。对计算能力要求较高。

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 中,底面
中,底面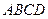 是矩形.已知
是矩形.已知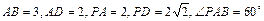 .
.
 平面
平面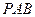 ;
;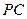 与
与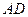 所成的角的大小;
所成的角的大小;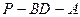 的大小.
的大小.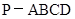 中,底面
中,底面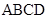 是菱形,
是菱形,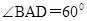 ,
,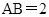 ,
,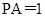 ,
,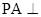 平面
平面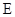 是
是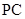 的中点,
的中点, 是
是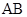 的中点.
的中点. 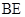 ∥平面
∥平面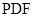 ;
;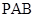 ;
;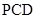 所成的锐二面角的大小.
所成的锐二面角的大小.
 中,底面
中,底面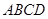 是矩形.已知
是矩形.已知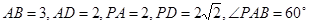 .
.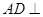 平面
平面 ;
;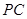 与
与 所成的角的大小;
所成的角的大小;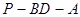 的大小.
的大小.
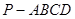 中,底面
中,底面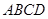 是正方形,侧棱
是正方形,侧棱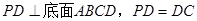 ,
,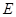 为
为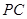 中点,作
中点,作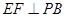 交
交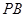 于
于
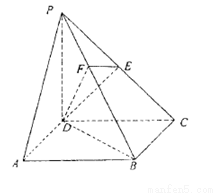
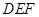 与平面
与平面 所成的锐二面角的正弦值。
所成的锐二面角的正弦值。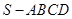 中,底面
中,底面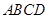 为平行四边形,
为平行四边形,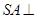 平面
平面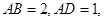

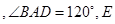 在棱
在棱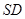 上.
上.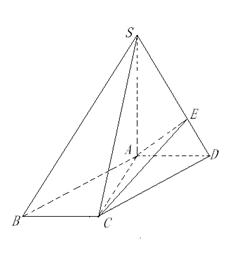
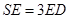 时,求证
时,求证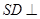 平面
平面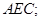
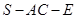 的大小为
的大小为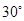 时,求直线
时,求直线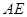 与平面
与平面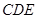 所成角的正弦值.
所成角的正弦值.