题目内容
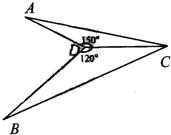 如图,∠ADC=150°,∠BDC=120°,AD=1,BD=
如图,∠ADC=150°,∠BDC=120°,AD=1,BD=| 3 |
分析:先作出A在面BDC上的投影,再作出二面角B-CD-A的平面角,由二面角的大小已知可求得点A到面BDC的距离,再求出线段AB的长度,进而可得线面角的正弦值.
解答: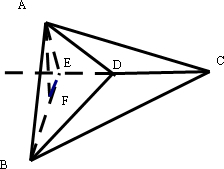 解:如图,作AF⊥面BDC于F,过F作FE⊥CD延长线于E,连接AE,由作图知AF⊥CD,
解:如图,作AF⊥面BDC于F,过F作FE⊥CD延长线于E,连接AE,由作图知AF⊥CD,
由线面垂直的判定定理知CD⊥面AEF,所以CD⊥AE,故∠AEF即二面角A-CD-B的平面角,故∠AEF=60°,
又∠ADC=150°,故∠ADE=30°,由AD=1,可得AE=
,DE=
∴EF=AE×cos60°=
×
=
,
AF=AEsin60°=
×
=
过B作BM⊥CD延长线于M,由∠BDC=120°得∠BDM=60°
又BD=
,故BM=
,DM=
,故M与E重合,
所以B,F,E,三点共线,则BF=
-
=
所以AB=
=
由上知∠ABF即线段AB与面BCD所成的角
sin∠ABF=
=
=
故应填
 解:如图,作AF⊥面BDC于F,过F作FE⊥CD延长线于E,连接AE,由作图知AF⊥CD,
解:如图,作AF⊥面BDC于F,过F作FE⊥CD延长线于E,连接AE,由作图知AF⊥CD,由线面垂直的判定定理知CD⊥面AEF,所以CD⊥AE,故∠AEF即二面角A-CD-B的平面角,故∠AEF=60°,
又∠ADC=150°,故∠ADE=30°,由AD=1,可得AE=
| 1 |
| 2 |
| ||
| 2 |
∴EF=AE×cos60°=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
AF=AEsin60°=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
过B作BM⊥CD延长线于M,由∠BDC=120°得∠BDM=60°
又BD=
| 3 |
| 3 |
| 2 |
| ||
| 2 |
所以B,F,E,三点共线,则BF=
| 3 |
| 2 |
| 1 |
| 4 |
| 5 |
| 4 |
所以AB=
| AF2+BF2 |
| ||
| 2 |
由上知∠ABF即线段AB与面BCD所成的角
sin∠ABF=
| AF |
| AB |
| ||||
|
| ||
| 14 |
故应填
| ||
| 14 |
点评:考查二面角,线面角的定义及相应平面角的作法.

练习册系列答案
相关题目
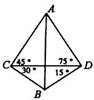 我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号). 如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是
如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是 (2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米).
(2012•肇庆二模)如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;找到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC=60°,∠ACB=15°,∠BCE=105°,∠CEB=45°,DC=CE=1(百米). 如图,为了测量河对岸A,B两点间的距离,某课外小组的同学在岸边选取C,D两点,测得CD=200m,∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,则A,B两点间的距离是( )
如图,为了测量河对岸A,B两点间的距离,某课外小组的同学在岸边选取C,D两点,测得CD=200m,∠ADC=105°,∠BDC=15°,∠BCD=120°,∠ACD=30°,则A,B两点间的距离是( )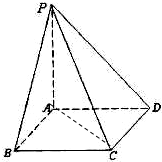 如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,
如图所示,PA⊥平面ABCD,底面ABCD为直角梯形,