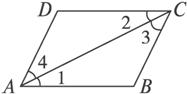
题目内容
用三段论的形式写出下列演绎推理．（1）若两角是对顶角，则该两角相等，所以若两角不相等，则该两角不是对顶角；
（2）矩形的对角线相等，正方形的是矩形，所以正方形的对角线相等；
（3）0.
| • |
| 3 |
| • |
| 3 |
| • |
| 2 |
（4）y=sinx（x∈R）是周期函数．
分析：要把一个定理写成三段论的形式，一定要根据定理的形式，分析定理所反映的一般情规律，即大前提；定理所对应的特殊情况与一般性定理之间的包含关系，即小前提．逐一对四个定理进行分析，分解，即可得到答案．
解答：解：（1）“两个角是对顶角，则两角相等”是大前提
“∠1和∠2不相等”是小前提
“∠1和∠2不是对顶角”为结论
（2）“每个矩形的对角线相等”是大前提
“正方形是矩形”是小前提
“正方形的对角线相等”是结论
（3）“所有的循环小数是有理数”是大前提
“0.
是循环小数”是小前提
“所以0.
是有理数”是结论
（4）“三角函数是周期函数”是大前提
“y=sinx是三角函数”是小前提
“y=sinx是周期函数”是结论．
“∠1和∠2不相等”是小前提
“∠1和∠2不是对顶角”为结论
（2）“每个矩形的对角线相等”是大前提
“正方形是矩形”是小前提
“正方形的对角线相等”是结论
（3）“所有的循环小数是有理数”是大前提
“0.
| • |
| 3 |
| • |
| 3 |
| • |
| 2 |
“所以0.
| • |
| 3 |
| • |
| 3 |
| • |
| 2 |
（4）“三角函数是周期函数”是大前提
“y=sinx是三角函数”是小前提
“y=sinx是周期函数”是结论．
点评：演绎推理的主要形式就是由大前提、小前提推出结论的三段论推理．三段论推理的依据用集合论的观点来讲就是：若集合M的所有元素都具有性质P，S是M的子集，那么S中所有元素都具有性质P．三段论的公式中包含三个判断：第一个判断称为大前提，它提供了一个一般的原理；第二个判断叫小前提，它指出了一个特殊情况；最后是根据两个判断做出的结论．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
ABCD.
ABCD为真.