题目内容
已知a>0,b∈R,函数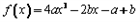 。
。
(Ⅰ)证明:当0≤x≤1时,
(i)函数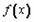 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;
(ii) +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;
(Ⅱ)若-1≤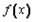 ≤1对x∈[0,1]恒成立,求a+b的取值范围。
≤1对x∈[0,1]恒成立,求a+b的取值范围。
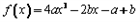 。
。(Ⅰ)证明:当0≤x≤1时,
(i)函数
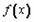 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;(ii)
 +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;(Ⅱ)若-1≤
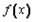 ≤1对x∈[0,1]恒成立,求a+b的取值范围。
≤1对x∈[0,1]恒成立,求a+b的取值范围。| 解:(Ⅰ) (ⅰ) 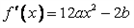 当b≤0时,  >0在0≤x≤1上恒成立, >0在0≤x≤1上恒成立,此时 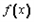 的最大值为: 的最大值为: =|2a-b|﹢a; =|2a-b|﹢a;当b>0时, 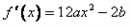 在0≤x≤1上的正负性不能判断, 在0≤x≤1上的正负性不能判断,此时  的最大值为: 的最大值为: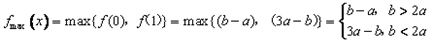 =|2a-b|﹢a; =|2a-b|﹢a;综上所述:函数  在0≤x≤1上的最大值为|2a-b|﹢a; 在0≤x≤1上的最大值为|2a-b|﹢a;(ⅱ) 要证 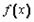 +|2a-b|﹢a≥0,即证 +|2a-b|﹢a≥0,即证 =﹣ =﹣ ≤|2a-b|﹢a. ≤|2a-b|﹢a.亦即证  在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a, 在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a,∵  , ,∴令 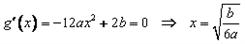 当b≤0时, 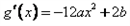 <0在0≤x≤1上恒成立, <0在0≤x≤1上恒成立,此时 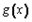 的最大值为: 的最大值为: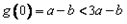 =|2a-b|﹢a; =|2a-b|﹢a;当b<0时,  在0≤x≤1上的正负性不能判断, 在0≤x≤1上的正负性不能判断,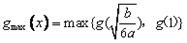 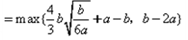  ≤|2a-b|﹢a; ≤|2a-b|﹢a;综上所述:函数 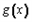 在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a. 在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a.即 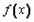 +|2a-b|﹢a≥0在0≤x≤1上恒成立。 +|2a-b|﹢a≥0在0≤x≤1上恒成立。 |
|
(Ⅱ)由(Ⅰ)知:函数 在0≤x≤1上的最大值为|2a-b|﹢a, 在0≤x≤1上的最大值为|2a-b|﹢a,且函数 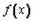 在0≤x≤1上的最小值比﹣(|2a-b|﹢a)要大 在0≤x≤1上的最小值比﹣(|2a-b|﹢a)要大∵﹣1≤  ≤1对x ≤1对x [0,1]恒成立, [0,1]恒成立,∴|2a-b|﹢a≤1 取b为纵轴,a为横轴.则可行域为:  和 和 ,目标函数为z=a+b. ,目标函数为z=a+b.作图如下:由图易得:当目标函数为z=a+b过P(1,2)时,有 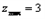 ∴所求a+b的取值范围为:  。 。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目