题目内容
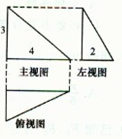 如图所示,一个三棱锥的三视图是三个直角三角形(单位:cm),则该三棱锥的外接球的表面积为
如图所示,一个三棱锥的三视图是三个直角三角形(单位:cm),则该三棱锥的外接球的表面积为29πcm2
29πcm2
.分析:几何体复原为底面是直角三角形,一条侧棱垂直底面直角顶点的三棱锥,扩展为长方体,长方体的对角线的长,就是外接球的直径,然后求其的表面积.
解答:解:由三视图复原几何体,几何体是底面是直角三角形,
一条侧棱垂直底面直角顶点的三棱锥;把它扩展为长方体,两者有相同的外接球,
它的对角线的长为球的直径,即
=2R,R=
.
该三棱锥的外接球的表面积为:该三棱锥的外接球的表面积为:4×π×(
)2=29π.
故答案为:29πcm2
一条侧棱垂直底面直角顶点的三棱锥;把它扩展为长方体,两者有相同的外接球,
它的对角线的长为球的直径,即
| 22+32+4 2 |
| ||
| 2 |
该三棱锥的外接球的表面积为:该三棱锥的外接球的表面积为:4×π×(
| ||
| 2 |
故答案为:29πcm2
点评:本题考查三视图,几何体的外接球的表面积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 (2013•烟台二模)如图所示,一个三棱锥的三视图是三个直角三角形 (单位:cm),则该三棱锥的外接球的表面积为
(2013•烟台二模)如图所示,一个三棱锥的三视图是三个直角三角形 (单位:cm),则该三棱锥的外接球的表面积为 如图所示,一个三棱锥的三视图是三个直角形,则该三棱锥的体积为
如图所示,一个三棱锥的三视图是三个直角形,则该三棱锥的体积为 .
.
