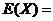题目内容
某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为| 2 |
| 3 |
| 1 |
| 12 |
分析:根据该毕业生得到面试的机会为0时的概率,做出得到乙、丙公司面试的概率,根据题意得到X的可能取值,结合变量对应的事件写出概率和做出期望.
解答:解:由题意知X为该毕业生得到面试的公司个数,则X的可能取值是0,1,2,3,
∵P(X=0)=
,
∴
(1-p)2 =
,
∴p=
,
P(X=1)=
×
×
+
×
×
+
×
×
=
P(X=2)=
×
×
+
×
×
+
×
×
=
,
P(X=3)=1-
-
-
=
,
∴E(X)=1×
+2×
+3×
=
,
故答案为:
∵P(X=0)=
| 1 |
| 12 |
∴
| 1 |
| 3 |
| 1 |
| 12 |
∴p=
| 1 |
| 2 |
P(X=1)=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 12 |
P(X=2)=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 12 |
P(X=3)=1-
| 1 |
| 12 |
| 4 |
| 12 |
| 5 |
| 12 |
| 2 |
| 12 |
∴E(X)=1×
| 4 |
| 12 |
| 5 |
| 12 |
| 2 |
| 12 |
| 5 |
| 3 |
故答案为:
| 5 |
| 3 |
点评:本题考查离散型随机变量的分布列和离散型随机变量的期望,考查生活中常见的一种题目背景,是一个基础题目.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
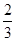 ,得到乙公司面试的概率为
,得到乙公司面试的概率为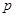 ,且两个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若
,且两个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若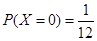 ,则随机变量X的数学期望
,则随机变量X的数学期望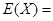
 ,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=
,得到乙、丙两公司面试的概率均为p,且三个公司是否让其面试是相互独立的.记X为该毕业生得到面试的公司个数.若P(X=0)=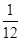 ,则随机变量X的数学期望E(X)=____
,则随机变量X的数学期望E(X)=____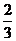 ,得到乙公司面试的概率为
,得到乙公司面试的概率为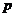 ,且三个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若
,且三个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若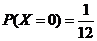 ,则随机变量X的数学期望
,则随机变量X的数学期望