题目内容
(理科)若函数f(x)=|sinx|(x≥0)的图象与直线y=kx仅有三个公共点,且其横坐标分别为α,β,γ(α<β<γ),给出下列结论:
①k=-cosγ;
②γ∈(π,
);
③γ=tanγ;
④sin2γ=
,
其中正确的结论是( )
①k=-cosγ;
②γ∈(π,
| 3π |
| 2 |
③γ=tanγ;
④sin2γ=
| 2γ |
| 1+γ2 |
其中正确的结论是( )
分析:可作出函数f(x)=|sinx|与直线y=kx仅有三个公共点的图象,利用导数与斜率的坐标公式可分别求得k,进一步分析即可得到答案.
解答:解:函数f(x)=|sinx|的图象与直线y=kx仅有三个公共点,其图象如下(k>0的情形):
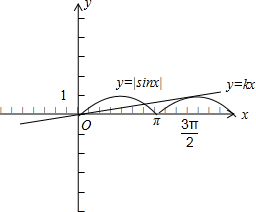
由图可知:
由图知,π<γ<
所以此时y=-sinx,由于直线在此段上与y=-sinx相切,切点处的导数为=-cosγ,故有k=-cosγ,①正确;
由图知,
<β<π<γ<
,故②正确,
∵直线y=kx与 y=-sinx 相切,
∴k=
,同时,由 y′=-cosx,
∴-
=-cosγ,所以 γ=tanγ,故③正确;
∴由万能公式可得sin2γ=
=
,故④正确.
故选D.

由图可知:
由图知,π<γ<
| 3π |
| 2 |
由图知,
| π |
| 2 |
| 3π |
| 2 |
∵直线y=kx与 y=-sinx 相切,
∴k=
| -sinγ |
| γ |
∴-
| sinγ |
| γ |
∴由万能公式可得sin2γ=
| 2tanγ |
| 1+tan2γ |
| 2γ |
| 1+γ2 |
故选D.
点评:本题考查考查正弦函数的图象,考查导数的几何意义与万能公式,属于难题

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 ,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是 .
,当x∈[0,1]时,f(x)=x,若在区间(-1,1]上,g(x)=f(x)-mx-m有两个零点,则实数m的取值范围是 .