题目内容
已知X的分布列为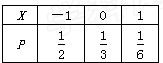 ,且Y=aX+3,EY=
,且Y=aX+3,EY=
,则a为( )
 ,且Y=aX+3,EY=
,且Y=aX+3,EY=| 7 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
分析:由期望的计算公式首先计算出EX,再由期望的性质,Y=aX+3,EY=aEX+3求出a即可.
解答:解:先求出EX=(-1)×
+0×
+1×
=-
.
再由Y=aX+3得EY=aEX+3.
∴
=a(-
)+3,解得a=2.
故选B.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
再由Y=aX+3得EY=aEX+3.
∴
| 7 |
| 3 |
| 1 |
| 3 |
故选B.
点评:本题考查离散型随机变量的期望及期望的性质,属基本运算的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
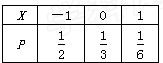 ,且Y=aX+3,EY=
,且Y=aX+3,EY= ,则a为
,则a为 ,且Y=aX+3,EY=
,且Y=aX+3,EY= ,则a为( )
,则a为( )