题目内容
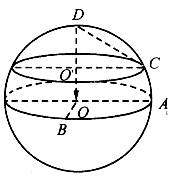
如图，设地球半径为R，点A、B在赤道上，O为地心，点C在北纬30°的纬线（O'为其圆心）上，且点A、C、D、O'、O共面，点D、O'、O共线．若∠AOB=90°，则异面直线AB与CD所成角的余弦值为（ ）
A．
B．
C．
D．
【答案】分析：先以OB、OA、OD所在直线为x轴、y轴、z轴建立空间直角坐标系；并求出各点的坐标，进而求出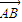
，
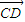的坐标，最后代入向量的夹角计算公式即可得到结论．
解答：解：分别以OB、OA、OD所在直线为x轴、y轴、z轴建立空间直角坐标系O-xyz，
易得A（0，R，0），B（R，0，0），C（0，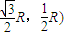
，D（0，0，R），
∴
，
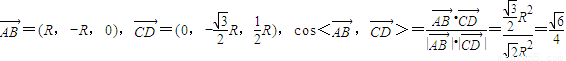即异面直线AB与CD所成角的余弦值为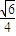
．
故选：A．
点评：本题主要考察用空间向量求直线间的夹角．用空间向量求直线间的夹角的关键在于线求出两向量的坐标，最后直接代入向量的夹角计算公式即可．
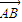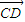，的坐标，最后代入向量的夹角计算公式即可得到结论．解答：解：分别以OB、OA、OD所在直线为x轴、y轴、z轴建立空间直角坐标系O-xyz，
易得A（0，R，0），B（R，0，0），C（0，
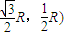，D（0，0，R），∴
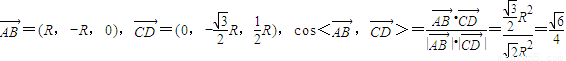，即异面直线AB与CD所成角的余弦值为
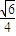．故选：A．
点评：本题主要考察用空间向量求直线间的夹角．用空间向量求直线间的夹角的关键在于线求出两向量的坐标，最后直接代入向量的夹角计算公式即可．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
（2007•成都一模）如图，设地球半径为R，点A、B在赤道上，O为地心，点C在北纬30°的纬线（O'为其圆心）上，且点A、C、D、O'、O共面，点D、O'、O共线．若∠AOB=90°，则异面直线AB与CD所成角的余弦值为（ ）
|
为其圆心）上，且点A、C、D、、O共面，点D、、O共线.若
，则异面直线AB与CD所成角的余弦值为 （ ） A．
B．
C．
D．
为其圆心）上，且点A、C、D、
，则异面直线AB与CD所成角的余弦值为 （ ） 
B．
D．
B．
C．
D．