题目内容
已知双曲线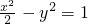 与射线y=
与射线y= (x≥0)公共点为P,过P作两条倾斜角互补且不重合的直线,它们与双曲线都相交且另一个交点分别为A,B(不同于P).
(x≥0)公共点为P,过P作两条倾斜角互补且不重合的直线,它们与双曲线都相交且另一个交点分别为A,B(不同于P).
(1)求点P到双曲线两条渐近线的距离之积;
(2)设直线PA斜率为k,求k的取值范围;
(3)求证直线AB的斜率为定值.
解:(1)由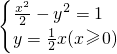 ,得P(2,1),
,得P(2,1),
双曲线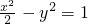 的渐近线方程是
的渐近线方程是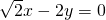 和
和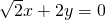 ,
,
点P(2,1)到两条渐近线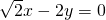 和
和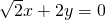 的距离分别是
的距离分别是
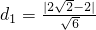 和
和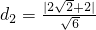 ,
,
∴点P到双曲线两条渐近线的距离之积
d1d2=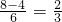 .
.
(2)设直线PA斜率为k,则PA的方程为:y-1=k(x-2),
即kx-y+1-2k=0,
由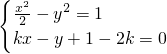 ,消去y,并整理,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,
,消去y,并整理,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,
∵直线PA与双曲线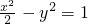 有两个交点,
有两个交点,
∴△=(8k2-4k)2-4(1-2k2)(8k-8k2-4)>0,
即k2-2k+1>0,
∴k≠1.
故k的取值范围是(-∞,1)∪(1,+∞).
(3)∵P(2,1),设A(x1,y1),B(x2,y2),
∵PA和PB是两条倾斜角互补且不重合的直线,
设PA斜率是m,则PB斜率是-m
则PA:y=m(x-2)+1,PB:y=-m(x-2)+1,
分别与双曲线方程联立,得
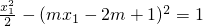 ,
,
(1-2m2)x12+(8m2-4m)x1+8m-8m2-4=0,
∵2是方程的一个根,
∴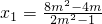 -2,
-2,
同理,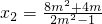 -2,
-2,
∴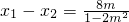 ,
,
∵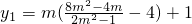 ,
,
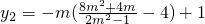 ,
,
∴y1-y2=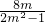 ,
,
∴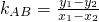 =
=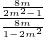 =-1.
=-1.
即直线AB的斜率为定值-1.
分析:(1)由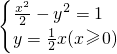 ,得P(2,1),双曲线
,得P(2,1),双曲线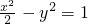 的渐近线方程是
的渐近线方程是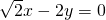 和
和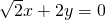 ,由此能求出点P到双曲线两条渐近线的距离之积.
,由此能求出点P到双曲线两条渐近线的距离之积.
(2)设直线PA斜率为k,则PA的方程为kx-y+1-2k=0,由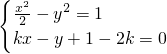 ,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,由直线PA与双曲线
,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,由直线PA与双曲线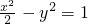 有两个交点,知△=(8k2-4k)2-4(1-2k2)(8k-8k2-4)>0,由此能求出k的取值范围.
有两个交点,知△=(8k2-4k)2-4(1-2k2)(8k-8k2-4)>0,由此能求出k的取值范围.
(3)P(2,1),设A(x1,y1),B(x2,y2),设PPA:y=m(x-2)+1,PB:y=-m(x-2)+1,分别与双曲线方程联立,得(1-2m2)x12+(8m2-4m)x1+8m-8m2-4=0,由2是方程的一个根,知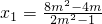 -2,同理,
-2,同理,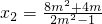 -2,所以
-2,所以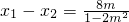 ,由
,由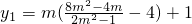 ,
,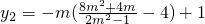 ,所以y1-y2=
,所以y1-y2=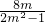 ,由此能够证明直线AB的斜率为定值-1.
,由此能够证明直线AB的斜率为定值-1.
点评:本题主要考查双曲线的标准方程,简单几何性质,直线与双曲线的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
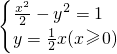 ,得P(2,1),
,得P(2,1),双曲线
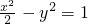 的渐近线方程是
的渐近线方程是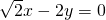 和
和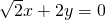 ,
,点P(2,1)到两条渐近线
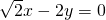 和
和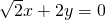 的距离分别是
的距离分别是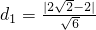 和
和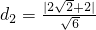 ,
,∴点P到双曲线两条渐近线的距离之积
d1d2=
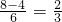 .
.(2)设直线PA斜率为k,则PA的方程为:y-1=k(x-2),
即kx-y+1-2k=0,
由
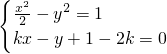 ,消去y,并整理,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,
,消去y,并整理,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,∵直线PA与双曲线
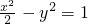 有两个交点,
有两个交点,∴△=(8k2-4k)2-4(1-2k2)(8k-8k2-4)>0,
即k2-2k+1>0,
∴k≠1.
故k的取值范围是(-∞,1)∪(1,+∞).
(3)∵P(2,1),设A(x1,y1),B(x2,y2),
∵PA和PB是两条倾斜角互补且不重合的直线,
设PA斜率是m,则PB斜率是-m
则PA:y=m(x-2)+1,PB:y=-m(x-2)+1,
分别与双曲线方程联立,得
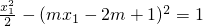 ,
,(1-2m2)x12+(8m2-4m)x1+8m-8m2-4=0,
∵2是方程的一个根,
∴
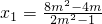 -2,
-2,同理,
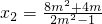 -2,
-2,∴
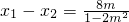 ,
,∵
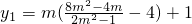 ,
,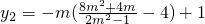 ,
,∴y1-y2=
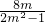 ,
,∴
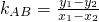 =
=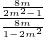 =-1.
=-1.即直线AB的斜率为定值-1.
分析:(1)由
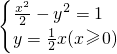 ,得P(2,1),双曲线
,得P(2,1),双曲线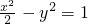 的渐近线方程是
的渐近线方程是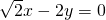 和
和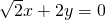 ,由此能求出点P到双曲线两条渐近线的距离之积.
,由此能求出点P到双曲线两条渐近线的距离之积.(2)设直线PA斜率为k,则PA的方程为kx-y+1-2k=0,由
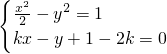 ,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,由直线PA与双曲线
,得(1-2k2)x2+(8k2-4k)x+8k-8k2-4=0,由直线PA与双曲线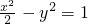 有两个交点,知△=(8k2-4k)2-4(1-2k2)(8k-8k2-4)>0,由此能求出k的取值范围.
有两个交点,知△=(8k2-4k)2-4(1-2k2)(8k-8k2-4)>0,由此能求出k的取值范围.(3)P(2,1),设A(x1,y1),B(x2,y2),设PPA:y=m(x-2)+1,PB:y=-m(x-2)+1,分别与双曲线方程联立,得(1-2m2)x12+(8m2-4m)x1+8m-8m2-4=0,由2是方程的一个根,知
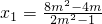 -2,同理,
-2,同理,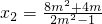 -2,所以
-2,所以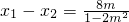 ,由
,由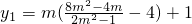 ,
,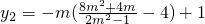 ,所以y1-y2=
,所以y1-y2=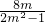 ,由此能够证明直线AB的斜率为定值-1.
,由此能够证明直线AB的斜率为定值-1.点评:本题主要考查双曲线的标准方程,简单几何性质,直线与双曲线的位置关系,双曲线的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
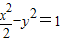 与射线y=
与射线y=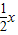 (x≥0)公共点为P,过P作两条倾斜角互补且不重合的直线,它们与双曲线都相交且另一个交点分别为A,B(不同于P).
(x≥0)公共点为P,过P作两条倾斜角互补且不重合的直线,它们与双曲线都相交且另一个交点分别为A,B(不同于P).