题目内容
在调查高中学生的近视情况中,某校高一年级145名男生中有60名近视,120名女生中有70名近视. 在检验这些高中学生眼睛近视是否与性别相关时,常采用的数据分析方法是( )
| A.期望与方差 | B.独立性检验 | C.正态分布 | D.二项分布列 |
B
解析试题分析:这是一个独立性检验应用题,处理本题时要注意根据已知构建方程计算出表格中男性近视与女性近视,近视的人数,并填入表格的相应位置.根据列联表及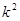 的计算公式,计算出
的计算公式,计算出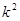 的值,并代入临界值表中进行比较,不难得到答案.
的值,并代入临界值表中进行比较,不难得到答案.
考点:独立性检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在验证吸烟与否与患肺炎与否有关的统计中,根据计算结果,认为这两件事情无关的可能性不足1%,那么 的一个可能取值为( )
的一个可能取值为( )
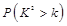 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
A.6.635 B.5.024 C.7.897 D.3.841
导弹发射的事故率为0.01,若发射10次,其出事故的次数为ξ,则下列结论正确的是
| A.P(ξ=k)=0.01k·0.9910-k | B.P(ξ=k)=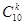 ·0.99k·0.0110-k ·0.99k·0.0110-k |
| C.Eξ=0.1 | D.Dξ=0.1 |
已知随机变量 服从正态分布
服从正态分布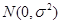 .则“
.则“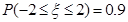 ”是“
”是“ ”的
”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
记集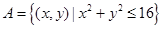 和集
和集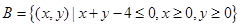 表示的平面区域分别为
表示的平面区域分别为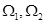 .若在区域
.若在区域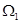 内任取一点
内任取一点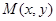 ,则点
,则点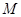 落在区域
落在区域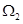 的概率为( )
的概率为( )
A. | B.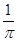 | C.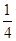 | D.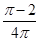 |
把颜色分别为红、黑、白的3个球随机地分给甲、乙、丙3人,每人分得1个球.事件“甲分得白球”与事件“乙分得白球”是( )
| A.对立事件 | B.不可能事件 |
| C.互斥事件 | D.必然事件 |
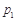 ,点数之和大于5的概率记为
,点数之和大于5的概率记为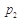 ,点数之和为偶数的概率记为
,点数之和为偶数的概率记为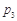 ,则
,则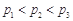
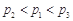
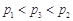
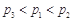
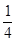 B.
B. C.
C.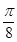 D.
D.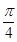
 是否存在自然数
是否存在自然数 ,使对任意
,使对任意 ,都有
,都有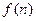 ?如果存在,求出
?如果存在,求出