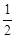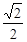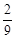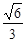题目内容
求经过点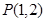 的直线,且使
的直线,且使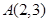 ,
,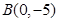 到它的距离相等的直线方程.( )
到它的距离相等的直线方程.( )
A.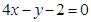 | B.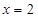 |
C.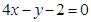 ,或 ,或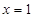 | D.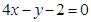 ,或 ,或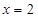 |
C
解析试题分析:当直线斜率不存在时,x=1显然符合条件;
当直线斜率存在时,显然A(2,3),B(0,-5)在所求直线同侧时,得到直线AB与所求的直线平行,kAB=4,所以所求的直线斜率为4,所以y-2=4(x-1),化简得:4x-y-2=0,所以满足条件的直线为4x-y-2=0,或x=1。
考点:直线方程的求法;点到直线的距离公式;直线方程的点斜式;两直线平行的条件。
点评:考查学生掌握两条直线平行时斜率的关系。在用点斜式求直线方程时,一定要想着讨论斜率是否存在。

练习册系列答案
相关题目
两直线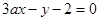 和
和 分别过定点A,B,则
分别过定点A,B,则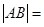 ( )
( )
A.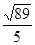 | B.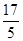 | C. | D.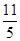 |
若直线经过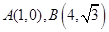 两点,则直线
两点,则直线 的倾斜角为
的倾斜角为
A.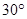 | B.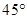 | C. | D.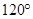 |
“直线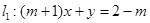 和
和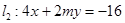 互相平行”的充要条件是“
互相平行”的充要条件是“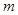 的值为( )”
的值为( )”
A.1或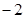 | B.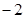 | C.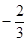 | D.1 |
与直线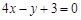 平行的抛物线
平行的抛物线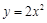 的切线方程是( ).
的切线方程是( ).
A.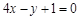 | B.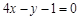 |
C.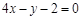 | D.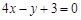 |
过点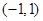 且斜率为
且斜率为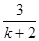 的直线
的直线 与直线
与直线 :
: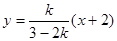 平行,则实数
平行,则实数 的值为( )
的值为( )
| A.1或-9 | B.1或9 | C.-9 | D.1 |
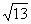
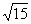

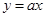 与
与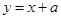 的是( )
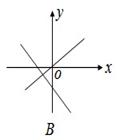
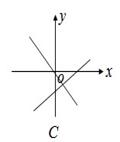
的是( )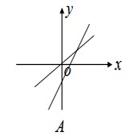
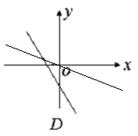
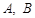 分别为椭圆
分别为椭圆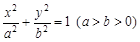 的左、右顶点,点
的左、右顶点,点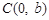 ,直线
,直线 :
: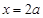 与
与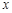 轴交于点D,与直线AC交于点P.若
轴交于点D,与直线AC交于点P.若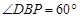 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )