题目内容
已知α:不等式|x-1|+|x+2|>m的解集为R;β:函数f(x)=log(5-2m)x在其定义域上是减函数.则α成立是β成立的
( )
( )
分析:根据不等式|x-1|+|x+2|>m的解集为R,由绝对值的几何意义知m<3,根据函数f(x)=log(5-2m)x在其定义域上是减函数,得到0<5-2m<1,得到两个条件之间的关系.
解答:解:∵不等式|x-1|+|x+2|>m的解集为R,
∴由绝对值的几何意义知m<3,
∵函数f(x)=log(5-2m)x在其定义域上是减函数,
∴0<5-2m<1
∴2<m<
,
∴α成立不能得到β一定成立,但是β成立时,α一定成立,
∴α是β的必要不充分条件,
故选C.
∴由绝对值的几何意义知m<3,
∵函数f(x)=log(5-2m)x在其定义域上是减函数,
∴0<5-2m<1
∴2<m<
| 5 |
| 2 |
∴α成立不能得到β一定成立,但是β成立时,α一定成立,
∴α是β的必要不充分条件,
故选C.
点评:本题考查的知识点是必要条件、充分条件与充要条件的判断,要判断p是q的什么条件,我们要先判断p⇒q与q⇒p的真假,再根据充要条件的定义给出结论.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
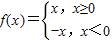 ,则不等式x+x•f(x)≤2的解集是 .
,则不等式x+x•f(x)≤2的解集是 .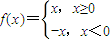 ,则不等式x+x•f(x)≤2的解集是 .
,则不等式x+x•f(x)≤2的解集是 .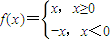 ,则不等式x+x•f(x)≤2的解集是 .
,则不等式x+x•f(x)≤2的解集是 .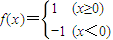 ,则不等式x+(x-3)f(x+1)≤1的解集是 .
,则不等式x+(x-3)f(x+1)≤1的解集是 .