题目内容
直线l1：x+my+4=0与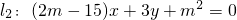
垂直，则m的值为
- A.3
- B.-3
- C.15
- D.-15
A
分析：利用直线的一般式方程与直线的垂直关系可得1×（2m-15）+m×3=0，即可求得答案．
解答：∵直线l1：x+my+4=0与l2：（2m-15）x+3y+m2=0垂直，
∴1×（2m-15）+m×3=0，
∴5m=15，
∴m=3．
故选A．
点评：本题考查直线的一般式方程与直线的垂直关系的应用，掌握规律是解决问题的关键，属于中档题．
分析：利用直线的一般式方程与直线的垂直关系可得1×（2m-15）+m×3=0，即可求得答案．
解答：∵直线l1：x+my+4=0与l2：（2m-15）x+3y+m2=0垂直，
∴1×（2m-15）+m×3=0，
∴5m=15，
∴m=3．
故选A．
点评：本题考查直线的一般式方程与直线的垂直关系的应用，掌握规律是解决问题的关键，属于中档题．
练习册系列答案
科学实验活动册系列答案
相关题目
直线l1：x+my+6=0和直线l2：（m-2）x+3y+2m=0互相平行，则m的取值为（ ）
| A、-1或3 | B、3 | C、-1 | D、1或-3 |