题目内容
某厂准备投资100万元生产A,B两种新产品,据测算,投产后的年收益,A产品是投入数的 ,B产品则是投入数开平方后的2倍,设投入B产品的数为x2(0<x≤10)万元.
,B产品则是投入数开平方后的2倍,设投入B产品的数为x2(0<x≤10)万元.
(Ⅰ)设两种产品的总收益为P(x),求P(x)的解析式;
(Ⅱ)怎样分配投入数,使总收益P(x)最大.
解:(Ⅰ)由题意,投入A产品的数为100-x2(0<x≤10)万元,
因为投产后的年收益,A产品是投入数的 ,B产品则是投入数开平方后的2倍,
,B产品则是投入数开平方后的2倍,
所以P(x)= (100-x2)+2x=-
(100-x2)+2x=- x2+2x+20(0<x≤10);
x2+2x+20(0<x≤10);
(Ⅱ)P(x)=- x2+2x+20=-
x2+2x+20=- (x-5)2+25
(x-5)2+25
∵0<x≤10,
∴x=5时,总收益P(x)最大为25万元.
此时,A产品投入75万元;B产品投入25万元.
分析:(Ⅰ)确定投入A产品的数,利用投产后的年收益,A产品是投入数的 ,B产品则是投入数开平方后的2倍,可得P(x)的解析式;
,B产品则是投入数开平方后的2倍,可得P(x)的解析式;
(Ⅱ)利用配方法,可求函数的最值,从而可得结论.
点评:本题考查函数模型的构建,考查配方法求函数最值,考查学生的计算能力,属于中档题.
因为投产后的年收益,A产品是投入数的
 ,B产品则是投入数开平方后的2倍,
,B产品则是投入数开平方后的2倍,所以P(x)=
 (100-x2)+2x=-
(100-x2)+2x=- x2+2x+20(0<x≤10);
x2+2x+20(0<x≤10);(Ⅱ)P(x)=-
 x2+2x+20=-
x2+2x+20=- (x-5)2+25
(x-5)2+25∵0<x≤10,
∴x=5时,总收益P(x)最大为25万元.
此时,A产品投入75万元;B产品投入25万元.
分析:(Ⅰ)确定投入A产品的数,利用投产后的年收益,A产品是投入数的
 ,B产品则是投入数开平方后的2倍,可得P(x)的解析式;
,B产品则是投入数开平方后的2倍,可得P(x)的解析式;(Ⅱ)利用配方法,可求函数的最值,从而可得结论.
点评:本题考查函数模型的构建,考查配方法求函数最值,考查学生的计算能力,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
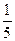 ,B产品则是总投入开平方
,B产品则是总投入开平方 后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大? ,B产品则是总投入开平方后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
,B产品则是总投入开平方后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?