题目内容
20.△ABC的内角A,B,C的对边分别是a,b,c,若B=2A,a=1,b=$\sqrt{3}$,则边c=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 2或1 |
分析 利用正弦定理列出关系式,将B=2A,a,b的值代入,利用二倍角的正弦函数公式化简,整理求出cosA的值,再由a,b及cosA的值,利用余弦定理即可求出c的值.
解答 解:∵B=2A,a=1,b=$\sqrt{3}$,
∴由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$得:$\frac{1}{sinA}=\frac{\sqrt{3}}{sinB}=\frac{\sqrt{3}}{sin2A}=\frac{\sqrt{3}}{2sinAcosA}$,
∴cosA=$\frac{\sqrt{3}}{2}$,
由余弦定理得:a2=b2+c2-2bccosA,即1=3+c2-3c,
解得:c=2或c=1(经检验不合题意,舍去),
则c=2.
故选:B.
点评 此题考查了正弦、余弦定理,二倍角的正弦函数公式,熟练掌握定理是解本题的关键,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
11.如图,若N=2015时,则输出的数等于( )
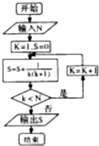

| A. | $\frac{2015}{2014}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2016}$ |
8.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(x,y).则“x=-2且y=-4”是“$\overrightarrow{a}$∥$\overrightarrow{b}$”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
5.复数z满足z•i=3-i,则在复平面内,复数z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.已知函数$f(x)=\frac{{sinx+cosx+|{sinx-cosx}|}}{2}$,则下列结论正确的是( )
| A. | f(x)是奇函数 | B. | f(x)在$[{0,\frac{π}{2}}]$上递增 | C. | f(x)是周期函数 | D. | f(x)的值域为[-1,1] |
 ,则
,则 ( )
( ) B.
B.
 D
D