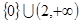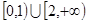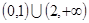题目内容
已知全集U=R,集合A={x|x2+(a-1)x-a>0},
B={x|(x+a)(x+b)>0(a≠b)},M={x|x2-2x-3≤0}.
(1)若∁UB=M,求a,b的值;
(2)若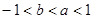 ,求A∩B;
,求A∩B;
(3)若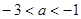 ,且
,且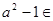 ∁UA,求实数
∁UA,求实数 的取值范围.
的取值范围.
B={x|(x+a)(x+b)>0(a≠b)},M={x|x2-2x-3≤0}.
(1)若∁UB=M,求a,b的值;
(2)若
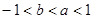 ,求A∩B;
,求A∩B;(3)若
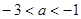 ,且
,且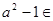 ∁UA,求实数
∁UA,求实数 的取值范围.
的取值范围.(1) =1,
=1, =-3,或
=-3,或 =-3,
=-3, =1.
=1.
(2) A∩B={ |
| <-
<- 或
或 >1}.(3)
>1}.(3)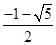 ≤
≤ ≤-
≤-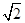 .
.
 =1,
=1, =-3,或
=-3,或 =-3,
=-3, =1.
=1.(2) A∩B={
 |
| <-
<- 或
或 >1}.(3)
>1}.(3)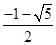 ≤
≤ ≤-
≤-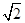 .
.(1)根据∁UB=M可知( +
+ )(
)( +
+ )=(
)=( +1)(
+1)( -3),从而求出a,b值.
-3),从而求出a,b值.
(2)根据-1< <
< <1可知方程(x+a)(x+b)=0的两根的大小关系,再根据二次函数,二次方程,二次不等式之间的对应关系可求出B,进而可求出A交B.
<1可知方程(x+a)(x+b)=0的两根的大小关系,再根据二次函数,二次方程,二次不等式之间的对应关系可求出B,进而可求出A交B.
(3)求出∁UA={x|1≤ ≤-
≤- },然后利用
},然后利用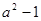 ∈∁UA,可得1≤
∈∁UA,可得1≤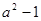 ≤-
≤- ,解此不等式可得a的取值范围.
,解此不等式可得a的取值范围.
解:由题意,A={ |(
|( +
+ )(
)( -1) >0},
-1) >0},
∁UB={ |(
|( +
+ )(
)( +
+ )≤0},
)≤0},
M={ |(
|( +1)(
+1)( -3)≤0}.
-3)≤0}.
(1)若∁UB=M,则( +
+ )(
)( +
+ )=(
)=( +1)(
+1)( -3),
-3),
所以 =1,
=1, =-3,或
=-3,或 =-3,
=-3, =1.
=1.
(2)若-1< <
< <1,则-1<-
<1,则-1<- <-
<- <1,
<1,
所以A={ |
| <-
<- 或
或 >1}, B={
>1}, B={ |
| <-
<- 或
或 >-
>- }.
}.
故A∩B={ |
| <-
<- 或
或 >1}.
>1}.
(3)若-3< <-1,则1<-
<-1,则1<- <3,
<3,
所以A={ |
| <1或
<1或 >-
>- },∁UA={x|1≤
},∁UA={x|1≤ ≤-
≤- }.
}.
又由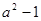 ∈∁UA,得1≤
∈∁UA,得1≤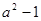 ≤-
≤- ,解得:
,解得: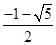 ≤
≤ ≤-
≤-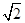 .
.
 +
+ )(
)( +
+ )=(
)=( +1)(
+1)( -3),从而求出a,b值.
-3),从而求出a,b值.(2)根据-1<
 <
< <1可知方程(x+a)(x+b)=0的两根的大小关系,再根据二次函数,二次方程,二次不等式之间的对应关系可求出B,进而可求出A交B.
<1可知方程(x+a)(x+b)=0的两根的大小关系,再根据二次函数,二次方程,二次不等式之间的对应关系可求出B,进而可求出A交B.(3)求出∁UA={x|1≤
 ≤-
≤- },然后利用
},然后利用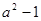 ∈∁UA,可得1≤
∈∁UA,可得1≤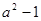 ≤-
≤- ,解此不等式可得a的取值范围.
,解此不等式可得a的取值范围.解:由题意,A={
 |(
|( +
+ )(
)( -1) >0},
-1) >0},∁UB={
 |(
|( +
+ )(
)( +
+ )≤0},
)≤0},M={
 |(
|( +1)(
+1)( -3)≤0}.
-3)≤0}.(1)若∁UB=M,则(
 +
+ )(
)( +
+ )=(
)=( +1)(
+1)( -3),
-3),所以
 =1,
=1, =-3,或
=-3,或 =-3,
=-3, =1.
=1.(2)若-1<
 <
< <1,则-1<-
<1,则-1<- <-
<- <1,
<1,所以A={
 |
| <-
<- 或
或 >1}, B={
>1}, B={ |
| <-
<- 或
或 >-
>- }.
}.故A∩B={
 |
| <-
<- 或
或 >1}.
>1}.(3)若-3<
 <-1,则1<-
<-1,则1<- <3,
<3,所以A={
 |
| <1或
<1或 >-
>- },∁UA={x|1≤
},∁UA={x|1≤ ≤-
≤- }.
}.又由
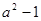 ∈∁UA,得1≤
∈∁UA,得1≤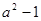 ≤-
≤- ,解得:
,解得: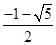 ≤
≤ ≤-
≤-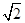 .
.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
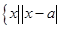 <
<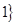 ,集合B=
,集合B=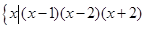 >
>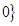 ,若
,若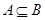 ,求实数
,求实数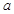 的取值范围.
的取值范围.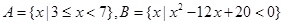 ,
, 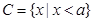 .
.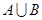 和
和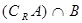 ;(2)若
;(2)若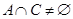 ,求
,求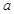 的取值范围.
的取值范围.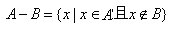 ,若
,若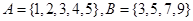 ,则A-B等于( )
,则A-B等于( ) ,
, ,
, ,则
,则 ( )
( )



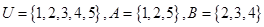 ,则
,则 ( )
( )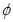
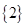
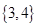
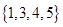
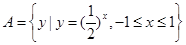 ,
,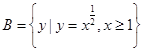 ,则
,则 .
.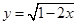 的定义域为集合
的定义域为集合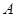 ,函数
,函数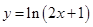 的定义域为集合
的定义域为集合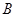 ,则
,则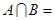 ( )
( )



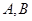 是非空集合,定义
是非空集合,定义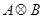 ={
={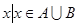 且
且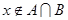 },己知集合
},己知集合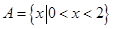 ,
, ,则
,则