题目内容
曲线
在点（－1，－3）处的切线方程是（ ）
A． | B． | C． | D． |
D
解析试题分析：由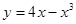
得
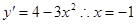时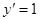
，所以切线斜率
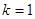，切线方程为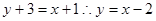
考点：函数求导及几何意义
点评：几何意义：函数在某一点处的导数值等于该点处的切线斜率
练习册系列答案
相关题目
如图，由函数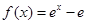
的图象，直线
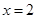及x轴所围成的阴影部分面积等于（ ）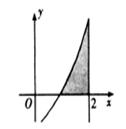
A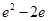． | B． |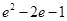
C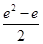． | D． |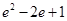
曲线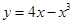
在点（－1，－3）处的切线方程是（ ）
A． | B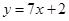． | C． | D． |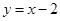
若
，则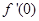
等于 （ ）
| A．－2 | B．－4 | C．2 | D．0 |
若
，则
( )
| A．0 | B．1 | C．2 | D．3 |
已知函数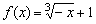
，则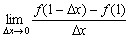
的值为（ ）
A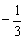． | B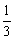． | C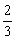． | D． |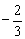
已知函数
与
轴切于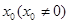
点,且极小值为
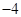,则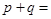
（ ）
| A．12 | B．13 | C．15 | D．16 |
某质点按规律
（
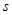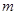单位：
，
单位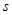：）作变速直线运动，则该质点在
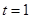时的瞬时速度为（ ）
A．2 | B．3 | C．4 | D．5 |
由直线
，曲线
及
轴所围图形的面积为（ ）
A． | B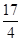． | C． | D． |