题目内容
在空间中,“经过点P(x0,y0,z0),法向量为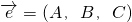 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x0)+B(y-y0)+C(z-z0)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x0)+B(y-y0)+C(z-z0)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是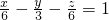 ,则由这两平面所成的二面角的正弦值是
,则由这两平面所成的二面角的正弦值是
- A.

- B.

- C.
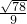
- D.

A
分析:由定义得出两直线的法向量,数量积公式求出法向量的夹角余弦,利用同角三角函数的关系求出其正弦即可选出正确答案
解答:由题意,平面α,β的法向量分别是 ,
, ,
,
所以 ,
,
故选A
点评:本题考查用空间向量求平面间的夹角,解题的关键是求出两个平面的法向量且掌握了法向量的夹角即两平面的夹角或是其补角,此类题规律固定,属于易题.
分析:由定义得出两直线的法向量,数量积公式求出法向量的夹角余弦,利用同角三角函数的关系求出其正弦即可选出正确答案
解答:由题意,平面α,β的法向量分别是
 ,
, ,
,所以
 ,
,故选A
点评:本题考查用空间向量求平面间的夹角,解题的关键是求出两个平面的法向量且掌握了法向量的夹角即两平面的夹角或是其补角,此类题规律固定,属于易题.

练习册系列答案
相关题目
 的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x)+B(y-y)+C(z-z)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是
的平面的方程(即平面上任意一点的坐标(x,y,z)满足的关系)是:A(x-x)+B(y-y)+C(z-z)=0”.如果给出平面α的方程是x-y+z=1,平面β的方程是 ,则由这两平面所成的二面角的正弦值是( )
,则由这两平面所成的二面角的正弦值是( )


