题目内容
求所有的素数对(p,q),使得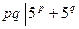 .
.
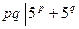 .
.见解析
若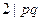 ,不妨设
,不妨设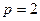 ,则
,则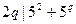 ,故
,故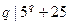 .
.
由Fermat小定理,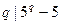 ,得
,得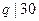 ,即
,即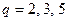 .易验证素数对
.易验证素数对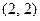 不合要求,
不合要求,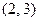 ,
,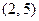 合乎要求.
合乎要求. 

若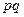 为奇数且
为奇数且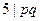 ,不妨设
,不妨设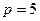 ,则
,则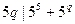 ,故
,故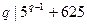 .
.
当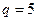 时素数对
时素数对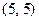 合乎要求,当
合乎要求,当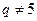 时,由Fermat小定理有
时,由Fermat小定理有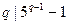 ,故
,故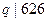 .由于
.由于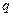 为奇素数,而626的奇素因子只有313,所以
为奇素数,而626的奇素因子只有313,所以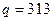 .经检验素数对
.经检验素数对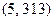 合乎要求.
合乎要求.
若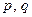 都不等于2和5,则有
都不等于2和5,则有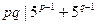 ,故
,故
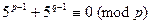 . ①
. ①
由Fermat小定理,得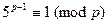 , ②
, ②
故由①,②得
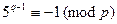 . ③
. ③
设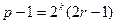 ,
,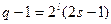 ,其中
,其中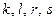 为正整数.
为正整数.
若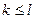 ,则由②,③易知
,则由②,③易知
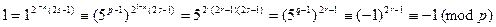 ,
,
这与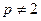 矛盾!所以
矛盾!所以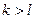 .
. 

同理有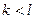 ,矛盾!即此时不存在合乎要求的
,矛盾!即此时不存在合乎要求的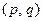 .
.
综上所述,所有满足题目要求的素数对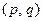 为
为
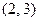 ,
,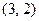 ,
,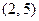 ,
,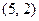 ,
,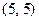 ,
,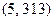 及
及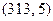 .
.
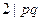 ,不妨设
,不妨设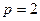 ,则
,则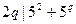 ,故
,故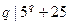 .
.由Fermat小定理,
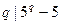 ,得
,得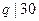 ,即
,即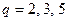 .易验证素数对
.易验证素数对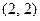 不合要求,
不合要求,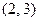 ,
,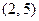 合乎要求.
合乎要求. 

若
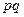 为奇数且
为奇数且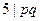 ,不妨设
,不妨设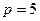 ,则
,则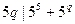 ,故
,故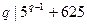 .
.当
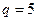 时素数对
时素数对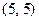 合乎要求,当
合乎要求,当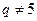 时,由Fermat小定理有
时,由Fermat小定理有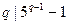 ,故
,故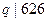 .由于
.由于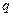 为奇素数,而626的奇素因子只有313,所以
为奇素数,而626的奇素因子只有313,所以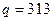 .经检验素数对
.经检验素数对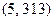 合乎要求.
合乎要求.若
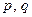 都不等于2和5,则有
都不等于2和5,则有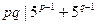 ,故
,故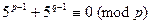 . ①
. ①由Fermat小定理,得
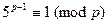 , ②
, ②故由①,②得
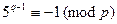 . ③
. ③设
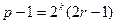 ,
,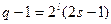 ,其中
,其中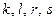 为正整数.
为正整数.若
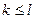 ,则由②,③易知
,则由②,③易知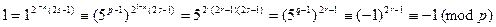 ,
,这与
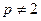 矛盾!所以
矛盾!所以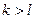 .
. 

同理有
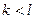 ,矛盾!即此时不存在合乎要求的
,矛盾!即此时不存在合乎要求的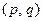 .
.综上所述,所有满足题目要求的素数对
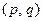 为
为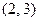 ,
,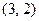 ,
,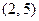 ,
,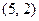 ,
,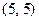 ,
,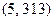 及
及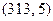 .
.
练习册系列答案
相关题目

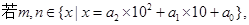 其中
其中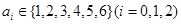 ,并且
,并且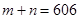 ,则实数对
,则实数对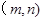 表示平面上不同点的个数是
表示平面上不同点的个数是