题目内容
微山县第一中学学生篮球队假期集训,集训前共有6个篮球,其中3个是新球(即没有用过的球),3个是旧球(即至少用过一次的球).每次训练,都从中任意取出2个球,用完后放回.(1)设第一次训练时取到的新球个数为ξ,求ξ的分布列;
(2)求第二次训练时恰好取到一个新球的概率.
【答案】分析:(1)ξ的所有可能取值为0,1,2,设“第一次训练时取到i个新球(即ξ=i)”为事件Ai(i=0,1,2),求出相应的概率,可得ξ的分布列与数学期望;
(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件B,则“第二次训练时恰好取到一个新球”就是事件AB+A1B+A2B.而事件AB、A1B、A2B互斥,由此可得结论.
解答:解:(1)ξ的所有可能取值为0,1,2
设“第一次训练时取到i个新球(即ξ=i)”为事件Ai(i=0,1,2).
因为集训前共有6个篮球,其中3个是新球,3个是旧球,所以
P(A)=P(ξ=0)=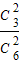 =
= ;P(A1)=P(ξ=1)=
;P(A1)=P(ξ=1)= =
= ;P(A2)=P(ξ=2)=
;P(A2)=P(ξ=2)=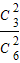 =
= ,
,
所以ξ的分布列为
ξ的数学期望为Eξ=0× +1×
+1× +2×
+2× =1;
=1;
(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件B,
则“第二次训练时恰好取到一个新球”就是事件AB+A1B+A2B,而事件AB、A1B、A2B互斥,
所以P(AB+A1B+A2B)=P(AB)+P(A1B)+P(A2B)=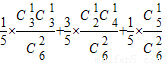 =
=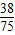
点评:本题考查概率的求法,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出概率是关键.
(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件B,则“第二次训练时恰好取到一个新球”就是事件AB+A1B+A2B.而事件AB、A1B、A2B互斥,由此可得结论.
解答:解:(1)ξ的所有可能取值为0,1,2
设“第一次训练时取到i个新球(即ξ=i)”为事件Ai(i=0,1,2).
因为集训前共有6个篮球,其中3个是新球,3个是旧球,所以
P(A)=P(ξ=0)=
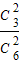 =
= ;P(A1)=P(ξ=1)=
;P(A1)=P(ξ=1)= =
= ;P(A2)=P(ξ=2)=
;P(A2)=P(ξ=2)=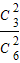 =
= ,
,所以ξ的分布列为
| ξ | 1 | 2 | |
| P |  |  |  |
 +1×
+1× +2×
+2× =1;
=1;(2)设“从6个球中任意取出2个球,恰好取到一个新球”为事件B,
则“第二次训练时恰好取到一个新球”就是事件AB+A1B+A2B,而事件AB、A1B、A2B互斥,
所以P(AB+A1B+A2B)=P(AB)+P(A1B)+P(A2B)=
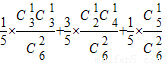 =
=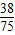
点评:本题考查概率的求法,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出概率是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
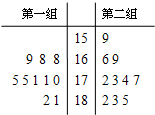 (2013•丰台区二模)高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示(如图).
(2013•丰台区二模)高三某班20名男生在一次体检中被平均分成两个小组,第一组和第二组学生身高(单位:cm)的统计数据用茎叶图表示(如图).