题目内容
已知椭圆 的方程为
的方程为 ,点
,点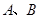 分别为其左、右顶点,点
分别为其左、右顶点,点 分别为其左、右焦点,以点
分别为其左、右焦点,以点 为圆心,
为圆心, 为半径作圆
为半径作圆 ;以点
;以点 为圆心,
为圆心, 为半径作圆
为半径作圆 ;若直线
;若直线 被圆
被圆 和圆
和圆 截得的弦长之比为
截得的弦长之比为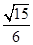 ;
;
(1)求椭圆 的离心率;
的离心率;
(2)己知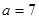 ,问是否存在点
,问是否存在点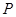 ,使得过
,使得过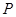 点有无数条直线被圆
点有无数条直线被圆 和圆
和圆 截得的弦长之比为
截得的弦长之比为 ;若存在,请求出所有的
;若存在,请求出所有的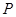 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

【答案】
解:(1)由 ,得直线
,得直线 的倾斜角为
的倾斜角为 ,
,
则点 到直线
到直线 的距离
的距离 ,
,
故直线 被圆
被圆 截得的弦长为
截得的弦长为 ,
,
直线 被圆
被圆 截得的弦长为
截得的弦长为 , (3分)
, (3分)
据题意有: ,即
,即 , (5分)
, (5分)
化简得: ,
,
解得: 或
或 ,又椭圆的离心率
,又椭圆的离心率 ;
;
故椭圆 的离心率为
的离心率为 .(7分)
.(7分)
(2)假设存在,设 点坐标为
点坐标为 ,过
,过 点的直线为
点的直线为 ;
;
当直线 的斜率不存在时,直线
的斜率不存在时,直线 不能被两圆同时所截;
不能被两圆同时所截;
故可设直线 的方程为
的方程为 ,
,
则点 到直线
到直线 的距离
的距离 ,
,
由(1)有 ,得
,得 =
= ,
,
故直线 被圆
被圆 截得的弦长为
截得的弦长为 , (9分)
, (9分)
则点 到直线
到直线 的距离
的距离 ,
,
 ,故直线
,故直线 被圆
被圆 截得的弦长为
截得的弦长为 , (11分)
, (11分)
据题意有: ,即有
,即有 ,整理得
,整理得 ,
,
即
 ,两边平方整理成关于
,两边平方整理成关于 的一元二次方程得
的一元二次方程得
 , (13分)
, (13分)
关于 的方程有无穷多解,
的方程有无穷多解,
故有: ,
,
故所求点 坐标为(-1,0)或(-49,0).
(16分)
坐标为(-1,0)或(-49,0).
(16分)
(注设过P点的直线为 后求得P点坐标同样得分)
后求得P点坐标同样得分)
【解析】略

练习册系列答案
相关题目

 的方程为
的方程为 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b). ,求点
,求点 的坐标;
的坐标; 交椭圆
交椭圆 、
、 两点,交直线
两点,交直线 于点
于点 .若
.若 ,证明:
,证明: 的中点;
的中点; 、
、 满足
满足 ,写出求作点
,写出求作点