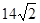题目内容
某圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392cm2,母线与轴的夹角为45°,则这个圆台的高为( )
| A、7 | ||
| B、14 | ||
| C、21 | ||
D、14
|
分析:画出圆台轴截面的示意图,找出圆台的上、下底面半径r、R,高h的关系,根据轴截面的面积求出r与h即可.
解答:解:设圆台的上、下底面半径分别为r、R,高为h,画出轴截面如图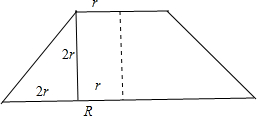 ;
;
根据题意得:
2πR=3×2πr,
∴R=3r,
又∵母线与轴的夹角为45°,
∴h=R-r=2r,
∴轴截面的面积为
(2r+2R)•h=
(2r+2×3r)•2r=8r2=392,
∴r=7,
∴圆台的高为h=2r=14;
故选:B.
 ;
;根据题意得:
2πR=3×2πr,
∴R=3r,
又∵母线与轴的夹角为45°,
∴h=R-r=2r,
∴轴截面的面积为
| 1 |
| 2 |
| 1 |
| 2 |
∴r=7,
∴圆台的高为h=2r=14;
故选:B.
点评:本题考查了圆台以及轴截面面积的有关计算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
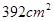 ,母线与轴的夹角为
,母线与轴的夹角为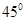 ,则这个圆台的高为
,则这个圆台的高为