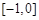题目内容
设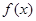 与
与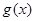 是定义在同一区间
是定义在同一区间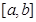 上的两个函数,若对任意
上的两个函数,若对任意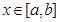 ,都有
,都有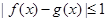 成立,则称
成立,则称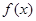 和
和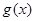 在
在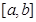 上是“密切函数”,区间
上是“密切函数”,区间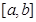 称为“密切区间”.若
称为“密切区间”.若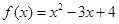 与
与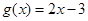 在
在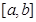 上是“密切函数”,则其“密切区间”可以是(
)
上是“密切函数”,则其“密切区间”可以是(
)
A. [1,4] B. [2,3] C. [2,4] D. [3,4]
【答案】
B
【解析】解:因为f(x)与g(x)在[a,b]上是“密切函数”,
则|f(x)-g(x)|≤1即|x2-3x+4-(2x-3)|≤1即|x2-5x+7|≤1,
化简得-1≤x2-5x+7≤1,因为x2-5x+7的△<0即与x轴没有交点,由开口向上得到x2-5x+7>0>-1恒成立;
所以由x2-5x+7≤1解得2≤x≤3,所以它的“密切区间”是[2,3]
故选B

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
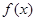 与
与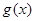 是定义在同一区间
是定义在同一区间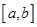 上的两个函数,若对任意的
上的两个函数,若对任意的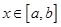 ,
,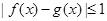 ,则称
,则称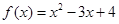 与
与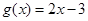 在
在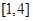 B.
B. 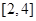 C.
C. 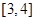 D.
D. 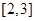
 与
与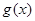 是定义在同一区间
是定义在同一区间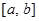 上的两个函数,若对任意
上的两个函数,若对任意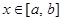 ,都有
,都有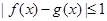 成立,则称
成立,则称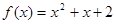 与
与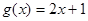 在
在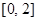 B.
B.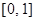 C.
C.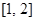 D.
D.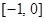
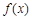 与
与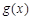 是定义在同一区间
是定义在同一区间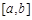 上的两个函数,若对任意
上的两个函数,若对任意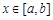 ,都有
,都有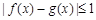 成立,则称
成立,则称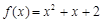 与
与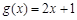 在
在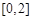 B.
B.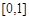 C.
C.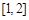 D.
D.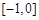
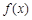 与
与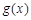 是定义在同一区间
是定义在同一区间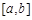 上的两个函数,若对任意
上的两个函数,若对任意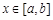 ,都有
,都有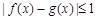 成立,则称
成立,则称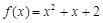 与
与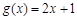 在
在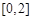 B.
B.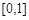 C.
C.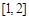 D.
D.