题目内容
已知数列{(1)求{
解析:(1)∵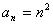 (n∈N※) ∴数列{
(n∈N※) ∴数列{ 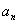 }的前n项和
}的前n项和 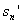
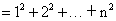
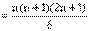 (证明从略)
(证明从略)
∴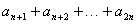
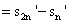
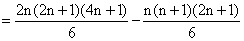
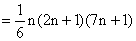
∴由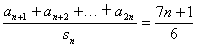 得
得 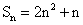 (n∈N※) ∴
(n∈N※) ∴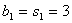
当n≥2时,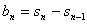
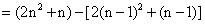
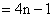
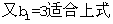 ∴bn=4n-1(n∈N※)
∴bn=4n-1(n∈N※)
(2)证:设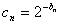 ,则
,则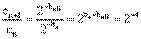 (常数)
(常数)
∴数列{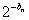 }是首项为2
}是首项为2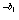 =
=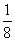 ,公比为
,公比为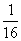 的等比数列
的等比数列
根据这一结论: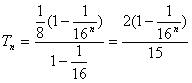
∴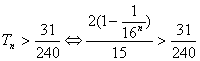
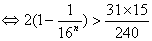

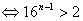
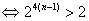 由此得4(n-1)>1即n≥2
由此得4(n-1)>1即n≥2
∴所求n的取值范围为{n|n≥2,n∈N※}.
∴
∴由
当n≥2时,
(2)证:设
∴数列{
根据这一结论:
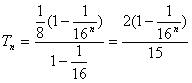
∴
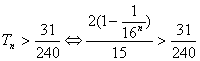
∴所求n的取值范围为{n|n≥2,n∈N※}.

练习册系列答案
 能考试全能100分系列答案
能考试全能100分系列答案
相关题目