题目内容
设p:实数m满足m2-4am+3a2<0(其中a<0);q:实数m满足方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线.若?p是?q的必要不充分条件,求实数a的取值范围.
解:设A={m|m2-4am+3a2<0,a<0}={m|3a<m<a,a<0},
因为方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线,
即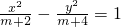 为双曲线,
为双曲线,
所以(m+4)(m+2)<0,…(4分)
设B={m|(m+4)(m+2)>0}={m|m<-4,或m>-2}
因为?p是?q的必要不充分条件,所以q是p的必要不充分条件.…(6分)
所以{m|3a<m<a,a<0}?{m|m<-4,或m>-2}…(8分)
则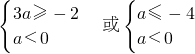 ,…(10分)
,…(10分)
解得:
故实数的取值范围为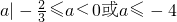 …(12分)
…(12分)
分析:通过解二次不等式化简命题p,利用双曲线方程的特点化简命题q,将?p是?q的必要不充分条件利用逆否命题的等价性转化为q是p的必要不充分条件,列出不等式求出a的范围.
点评:解决这种充要条件问题的方法是可以把命题转化为解方程或不等式的问题,观察两个集合的关系,进而得到两个命题的关系,高考一般出现选择与填空.
因为方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线,
即
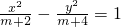 为双曲线,
为双曲线,所以(m+4)(m+2)<0,…(4分)
设B={m|(m+4)(m+2)>0}={m|m<-4,或m>-2}
因为?p是?q的必要不充分条件,所以q是p的必要不充分条件.…(6分)
所以{m|3a<m<a,a<0}?{m|m<-4,或m>-2}…(8分)
则
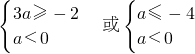 ,…(10分)
,…(10分)解得:

故实数的取值范围为
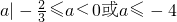 …(12分)
…(12分)分析:通过解二次不等式化简命题p,利用双曲线方程的特点化简命题q,将?p是?q的必要不充分条件利用逆否命题的等价性转化为q是p的必要不充分条件,列出不等式求出a的范围.
点评:解决这种充要条件问题的方法是可以把命题转化为解方程或不等式的问题,观察两个集合的关系,进而得到两个命题的关系,高考一般出现选择与填空.

练习册系列答案
相关题目
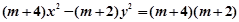 为双曲线,且
为双曲线,且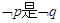 的必要不充分条件,求a的取值范围。
的必要不充分条件,求a的取值范围。