题目内容
函数
 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线 上,其中
上,其中 ,则
,则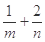 的最小值为 .
的最小值为 .

 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线 上,其中
上,其中 ,则
,则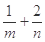 的最小值为 .
的最小值为 .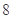 .
. 试题分析:函数

 的图象恒过定点
的图象恒过定点 ,由对数函数的图象特征知A(-2,-1)代入
,由对数函数的图象特征知A(-2,-1)代入 得,
得,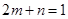 ,其中
,其中 ,
,所以
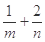 =(
=( )(
)(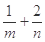 )=4+
)=4+
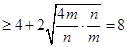 ,
,故
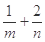 的最小值为8.
的最小值为8.点评:典型题,本题综合性较强,考查知识点多。利用已知条件得到
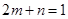 ,运用“1的代换”,创造了应用均值定理的条件。应用均值定理“一正、二定、三相等”。
,运用“1的代换”,创造了应用均值定理的条件。应用均值定理“一正、二定、三相等”。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
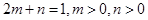 ,则
,则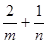 的最小值为 .
的最小值为 .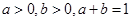 ,(1)求证:
,(1)求证: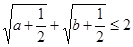
 的最小值
的最小值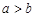 ,且
,且 ,则
,则 的最小值是 .
的最小值是 .  在由不等式组
在由不等式组 确定的平面区域内,则点
确定的平面区域内,则点 所在平面区域的面积是 。
所在平面区域的面积是 。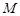 (2,2),
(2,2),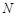 (
(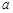 ,0),
,0),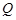 (0,
(0,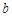 ),(
),(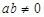 )共线,则
)共线,则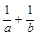 的值为( )
的值为( )


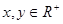 ,且2x+8y-xy=0则x+y的范围是 。
,且2x+8y-xy=0则x+y的范围是 。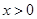 ,则
,则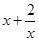 的最小值为 ;
的最小值为 ; ,且
,且 ,且
,且 恒成立,则实数
恒成立,则实数 取值范围是
取值范围是