题目内容
若直三棱柱的六个顶点在半径为R的同一球面上,且AC=CB=1,AA1=| 1 |
| 2 |
| 2 |
分析:根据直三棱柱的六个顶点在半径为R的同一球面上,由于∠ACB=90°,只要将直三棱柱补成长方体,长方体的对角线长即为球的直径,然后可求球的表面积.
解答:解:直三棱ABC-A1B1C1的各顶点都在同一球面上,
AC=CB=1,AB=
,∴∠ACB=90°
将直三棱柱补成长方体,长方体的对角线长即为球的直径
∵长方体的对角线长的平方为:
(2r)2=1 2+1 2+(
)2=
所以球的表面积为:4r2π=
故答案为:
.
AC=CB=1,AB=
| 2 |
将直三棱柱补成长方体,长方体的对角线长即为球的直径
∵长方体的对角线长的平方为:
(2r)2=1 2+1 2+(
| 1 |
| 2 |
| 9 |
| 4 |
所以球的表面积为:4r2π=
| 9π |
| 4 |
故答案为:
| 9π |
| 4 |
点评:本题考查球的体积和表面积,球的内接体问题,考查学生空间想象能力理解失误能力,是基础题.

练习册系列答案
相关题目
 ,
,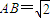 ,则该球的表面积为 .
,则该球的表面积为 .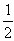 ,AB=
,AB=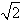 ,则该球的表面积为( )。
,则该球的表面积为( )。