题目内容
已知向量a=(sinx,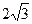 cosx),b=(2sinx,sinx),设
cosx),b=(2sinx,sinx),设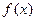 =a·b-1
=a·b-1
(1)求函数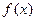 ,并求使函数取得最小值的x的集合
,并求使函数取得最小值的x的集合
(2)若方程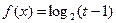 在x∈[
在x∈[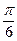 ,
,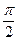 ]上有实数解,求实数
]上有实数解,求实数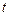 的取值范围.
的取值范围.
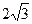 cosx),b=(2sinx,sinx),设
cosx),b=(2sinx,sinx),设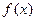 =a·b-1
=a·b-1(1)求函数
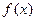 ,并求使函数取得最小值的x的集合
,并求使函数取得最小值的x的集合(2)若方程
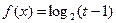 在x∈[
在x∈[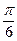 ,
,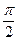 ]上有实数解,求实数
]上有实数解,求实数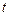 的取值范围.
的取值范围.{x|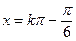 ,k∈Z},3≤t≤5
,k∈Z},3≤t≤5
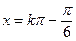 ,k∈Z},3≤t≤5
,k∈Z},3≤t≤5.解:(1)∵f (x)=a·b-1


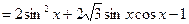
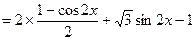
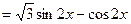
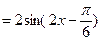 ,………………………………………4分
,………………………………………4分
∵当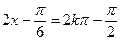 (k∈Z)即
(k∈Z)即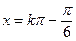 (k∈Z)时,函数f (x)取最小值,
(k∈Z)时,函数f (x)取最小值,
∴使函数f (x)取最小值的x的取值集合为{x|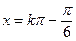 ,k∈Z}.…6分
,k∈Z}.…6分
(2)∵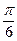 ≤x≤
≤x≤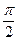 ,
,
∴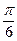 ≤2x-
≤2x-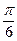 ≤
≤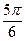 ,
,
∴ 1≤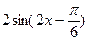 ≤2.…………………………………………………8分
≤2.…………………………………………………8分
要使原方程有解就需使 1≤log2(t-1)≤2,
解得 2≤t-1≤4,
∴ 3≤t≤5. ……………………………………………………………10分



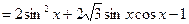
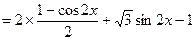
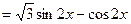
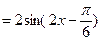 ,………………………………………4分
,………………………………………4分∵当
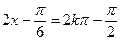 (k∈Z)即
(k∈Z)即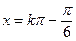 (k∈Z)时,函数f (x)取最小值,
(k∈Z)时,函数f (x)取最小值,∴使函数f (x)取最小值的x的取值集合为{x|
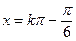 ,k∈Z}.…6分
,k∈Z}.…6分(2)∵
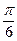 ≤x≤
≤x≤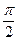 ,
,∴
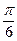 ≤2x-
≤2x-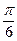 ≤
≤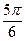 ,
,∴ 1≤
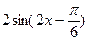 ≤2.…………………………………………………8分
≤2.…………………………………………………8分要使原方程有解就需使 1≤log2(t-1)≤2,
解得 2≤t-1≤4,
∴ 3≤t≤5. ……………………………………………………………10分

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
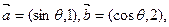 满足
满足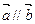 ,其中
,其中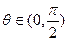 .
.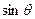 和
和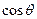 的值;
的值;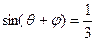 ,求
,求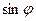 的值.
的值.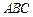 中,角
中,角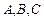 所对边分别为
所对边分别为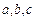 ,且
,且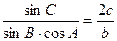 .(1)求角A;(2)若
.(1)求角A;(2)若
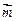
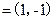 ,
,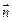 =
=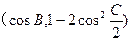 ,,试求
,,试求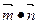 的取值范围.
的取值范围.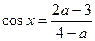 ,且x是第二、三象限角,则a的取值范围是_____
,且x是第二、三象限角,则a的取值范围是_____ ___
___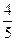 ,则m= .
,则m= . 且
且 ,则锐角
,则锐角 为( )
为( )



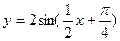 的周期,振幅,初相分别是___________
的周期,振幅,初相分别是___________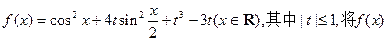 的最小值记为
的最小值记为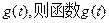 的单调递增区间为 ( )
的单调递增区间为 ( )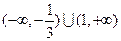
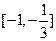
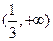

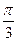 )的图象,可由y=sinx的图象经过下述哪种变换而得到:( )
)的图象,可由y=sinx的图象经过下述哪种变换而得到:( )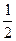 倍,纵坐标扩大到原来的3倍
倍,纵坐标扩大到原来的3倍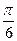 个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的
个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的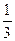 倍
倍