题目内容
设 、
、 、
、 是单位向量,且
是单位向量,且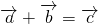 ,则
,则 与
与 的夹角为________.
的夹角为________.
60°
分析:向量表示错误,请给修改,谢谢
将已知等式变形,两边平方;利用向量模的平方等于向量的平方及向量的数量积公式求出 、
、 两个向夹角
两个向夹角
的余弦值,求出 、
、 的夹角,再由以
的夹角,再由以
 为邻边的平行四边形为菱形,即可求得
为邻边的平行四边形为菱形,即可求得  与
与 的夹角.
的夹角.
解答:设 、
、 两个向量的夹角为θ,由
两个向量的夹角为θ,由 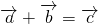 ,
, 、
、 、
、 是单位向量,
是单位向量,
两边平方可得 1+2 +1=1,即
+1=1,即  =-
=- .
.
即 1×1×cosθ=- ,∴θ=120°.
,∴θ=120°.
由题意可得,以
 为邻边的平行四边形为菱形,故
为邻边的平行四边形为菱形,故 与
与 的夹角为60°.
的夹角为60°.
故答案为 60°.
点评:本题考查要求两个向量的夹角关键要出现这两个向量的数量积,解决向量模的问题常采用将模平方转化为向量的平方,属于中档题.
分析:向量表示错误,请给修改,谢谢
将已知等式变形,两边平方;利用向量模的平方等于向量的平方及向量的数量积公式求出
 、
、 两个向夹角
两个向夹角的余弦值,求出
 、
、 的夹角,再由以
的夹角,再由以
 为邻边的平行四边形为菱形,即可求得
为邻边的平行四边形为菱形,即可求得  与
与 的夹角.
的夹角.解答:设
 、
、 两个向量的夹角为θ,由
两个向量的夹角为θ,由 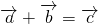 ,
, 、
、 、
、 是单位向量,
是单位向量,两边平方可得 1+2
 +1=1,即
+1=1,即  =-
=- .
.即 1×1×cosθ=-
 ,∴θ=120°.
,∴θ=120°.由题意可得,以

 为邻边的平行四边形为菱形,故
为邻边的平行四边形为菱形,故 与
与 的夹角为60°.
的夹角为60°.故答案为 60°.
点评:本题考查要求两个向量的夹角关键要出现这两个向量的数量积,解决向量模的问题常采用将模平方转化为向量的平方,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, 是单位向量,且
是单位向量,且 ,则向量
,则向量 ,
, ,
,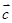 是单位向量,且
是单位向量,且 、
、 、
、 是单位向量,且
是单位向量,且 的最小值为
的最小值为 (B)
(B) (C)
(C) (D)
(D)