题目内容
6．已知数列{an}中，前m项依次构成首项为1，公差为-2的等差数列．第m+1项至第2m项依次构成首项为1，公比为$\frac{1}{2}$的等比数列，其中m≥3，m∈N*．（1）求am，a2m
（2）若对任意的n∈N*，都有an+2m=an．设数列{an}的前n项和为Sn，求S4m+3．
分析 （1）根据等差等比数列通项公式分段求出即可；
（2）结合an+2m=an把S4m+3转化为2S2m+a1+a2+a3，然后结合等差数列和等比数列的前m项和得答案．
解答 解：（1）当1≤n≤m时，an=1+（n-1）（-2）=-2n+3；
当m+1≤n≤2m时，${a}_{n}=1•（\frac{1}{2}）^{n-m-1}$，
综上，${a}_{n}=\left\{\begin{array}{l}{3-2n，1≤n≤m}\\{（\frac{1}{2}）^{n-m-1}，m+1≤n≤2m}\end{array}\right.$，
∴${a}_{m}=3-2m；{a}_{2m}=（\frac{1}{2}）^{m-1}$；
（2）S4m+3=S4m+a4m+1+a4m+2+a4m+3
=2S2m+a1+a2+a3=2[（a1+a2+…+am）+（am+1+am+2+…+a2m）]+a1+a2+a3
=$2[m+\frac{m（m-1）（-2）}{2}+\frac{1×（1-\frac{1}{{2}^{m}}）}{1-\frac{1}{2}}]$+（1-1-3）=$4m-2{m}^{2}-\frac{1}{{2}^{m-2}}+1$．
点评 本题考查了等差数列与等比数列的性质，考查了等差数列与等比数列的前n项和，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
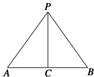已知一个正三棱锥P-ABC的正视图如图所示，若AC=BC=$\frac{3}{2}$，PC=$\sqrt{6}$，则此正三棱锥的表面积为9$\sqrt{3}$．