题目内容
设z∈C,且|z|=1,当|(z-1)(z-i)|最大时,z=( )
| A、-1 | ||||||||
| B、-i | ||||||||
C、-
| ||||||||
D、
|
分析:可设出复数的三角函数形式,再结合的三角函数知识进行求解.特别注意:令sinθ+cosθ=t,则sinθcosθ=
(t2-1)
| 1 |
| 2 |
解答:解:|z|=1,设z=cosθ+isinθ,则|(z-1)(z-i)|=2
令sinθ+cosθ=t,则sinθcosθ-sinθ-cosθ+1=
(t-1)2+
∴当t=-
即θ=
π时,|(z-1)(z-i)|取最大值,此时,z=-
-
i.
| sinθcosθ-sinθ-cosθ+1 |
令sinθ+cosθ=t,则sinθcosθ-sinθ-cosθ+1=
| 1 |
| 2 |
| 1 |
| 4 |
∴当t=-
| 2 |
| 5 |
| 4 |
| ||
| 2 |
| ||
| 2 |
点评:本题的综合性较强,是复数和三角函数的综合运用,在解题时要注意到换元的技巧.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
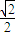 -
-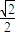 i
i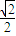 +
+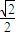 i
i