题目内容
(Ⅰ)用分期付款方式购买家用电器一件,价格为1150元,购买当天先付150元,以后每月这一天都交付50元,并加付欠款利息,月利率为1%.若交付150元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款多少元?(Ⅱ)用分期付款方式购买家用电器一件,价格为1150元,购买当天先付150元,以后每月这一天还款一次,每次还款数额相同,20个月还清,月利率为1%,按复利计息.若交付150元后的第一个月开始算分期付款的第一个月,全部欠款付清后,请问买这件家电实际付款
分析:(Ⅰ)购买当天先付150元后,所欠款数为1150-150,以后每月都交付50元,计算所需月数;分期付款的每一个月,计算应付欠款数,组成等差数列,求和,得分期付款总款数;从而得买这件家电实际付款数.
(Ⅱ)购买当天先付150元后,所欠款数为1150-150=1000(元),用20个月还清,月利率为1%,按复利计息,分期付款的总款数,是等比数列的前n项和,求出再得每个月应还款数,以及买这件家电实际付款数.
(Ⅱ)购买当天先付150元后,所欠款数为1150-150=1000(元),用20个月还清,月利率为1%,按复利计息,分期付款的总款数,是等比数列的前n项和,求出再得每个月应还款数,以及买这件家电实际付款数.
解答:解:(Ⅰ)购买当天先付150元后,所欠款数为1150-150=1000(元),
以后每月都交付50元,共需1000÷50=20(月);
分期付款的第一个月,应付欠款50+1000×1%=60(元),第二个月,应付欠款50+950×1%=59.5(元),…,第二十个月,应付欠款50+50×1%=50.5(元);
分期共付欠款为:60+59.5+…+50.5=
=1105(元);
所以,买这件家电实际付款为:1105+150=1255(元).
(Ⅱ)购买当天先付150元后,所欠款数为1150-150=1000(元),
用20个月还清,月利率为1%,按复利计息,分期付款的总款数为:
50×(1+1%)+50×(1+1%)2+…+50×(1+1%)20
=
=50.5×
=50.5×22.0=1111(元),
每次还款数额相同,为1111÷20=55.55(元);
所以,买这件家电实际付款为:1111+150=1261(元);
故答案为:每次还款55.55元,实际付款1261元.
以后每月都交付50元,共需1000÷50=20(月);
分期付款的第一个月,应付欠款50+1000×1%=60(元),第二个月,应付欠款50+950×1%=59.5(元),…,第二十个月,应付欠款50+50×1%=50.5(元);
分期共付欠款为:60+59.5+…+50.5=
| 20(60+50.5) |
| 2 |
所以,买这件家电实际付款为:1105+150=1255(元).
(Ⅱ)购买当天先付150元后,所欠款数为1150-150=1000(元),
用20个月还清,月利率为1%,按复利计息,分期付款的总款数为:
50×(1+1%)+50×(1+1%)2+…+50×(1+1%)20
=
| 50.5×[1-(1+1%)20] |
| 1-(1+1%) |
| 1-1.220 |
| -0.01 |
每次还款数额相同,为1111÷20=55.55(元);
所以,买这件家电实际付款为:1111+150=1261(元);
故答案为:每次还款55.55元,实际付款1261元.
点评:本题考查了等差、等比数列的综合应用;解题时须认真审题,细心解答,以免出错.

练习册系列答案
相关题目
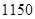 元,购买当天先付
元,购买当天先付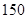 元,以后每月这一天都交付
元,以后每月这一天都交付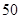 元,并加付欠款利息,月利率为
元,并加付欠款利息,月利率为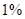 .若交付
.若交付 个月还清,月利率为
个月还清,月利率为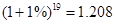 ,
,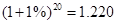 ,
,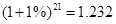 .
.