题目内容
有以下结论:①函数f(x)=log2(x+1)+log2(x-1)的定义域为(1,+∞);
②若幂函数y=f(x)的图象经过点(2,
| 2 |
③函数y=log2(1-x)的增区间是(-∞,1);
④函数y=3|x|的值域是[1,+∞).其中正确结论的序号是
分析:由真数大于零即x+1>0且x-1>0,求出解集是函数的定义域,判断出①对;利用图象上一点求出幂函数的解析式判断出②不对;由复合函数的单调性得出③不对;利用指数|x|≥0求出函数的值域得出④对.
解答:解:①、由x+1>0且x-1>0解得,x>1,则函数的定义域是(1,+∞),故①对;
②、设f(x)=xα,把(2,
)代入解得,α=
,故②不对;
③、因y=1-x在定义域上是减函数,而y=log2x在定义域上是增函数,故原函数的减区间是(-∞,1),
故③不对;
④、因|x|≥0,所以3|x|≥1,即函数的值域是[1,+∞),故④对.
故答案为:①④.
②、设f(x)=xα,把(2,
| 2 |
| 1 |
| 2 |
③、因y=1-x在定义域上是减函数,而y=log2x在定义域上是增函数,故原函数的减区间是(-∞,1),
故③不对;
④、因|x|≥0,所以3|x|≥1,即函数的值域是[1,+∞),故④对.
故答案为:①④.
点评:本题是有关基本初等函数的性质的综合题,考查了对数函数的定义域和单调性,幂函数的解析式以及奇偶性,指数函数的值域等知识,考查全面但是难度不大.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 ,则该函数为偶函数;
,则该函数为偶函数;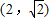 ,则该函数为偶函数;
,则该函数为偶函数;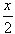 ,有以下结论:
,有以下结论: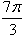 ]上是增函数;
]上是增函数;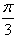 ]上是减函数;(5)f(x)的最大值是
]上是减函数;(5)f(x)的最大值是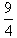 ;
;