题目内容
在等差数列中,若已知两项ap和aq,则等差数列的通项公式an=ap+(n-p)
.类似的,在等比数列中,若已知两项ap和aq(假设p>q),则等比数列的通项公式an=
| ap-aq |
| p-q |
ap•[
]n-p
| p-q |
| ||
ap•[
]n-p
.| p-q |
| ||
分析:设公比为m,根据等比数列的通项公式用ap和aq表示出公比m,然后代入an=ap•mn-p即可得到答案.
解答:解:在等比数列中,设公比为m,则ap=aq•mp-q,所以m=
,
所以an=ap•mn-p=ap•(
)n-p,
故答案为:ap•(
)n-p.
| p-q |
| ||
所以an=ap•mn-p=ap•(
| p-q |
| ||
故答案为:ap•(
| p-q |
| ||
点评:本题考查数列递推式、等比数列的通项公式,考查学生灵活运用知识解决问题的能力,熟练掌握等比数列通项公式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
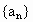 中,若
中,若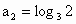 ,
,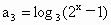 ,
,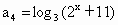 ,则x=________________.
,则x=________________.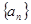 中,若
中,若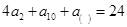 ,则
,则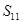 为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为
为定值”为真命题,由于印刷问题,括号处的数模糊不清,可推得括号内的数为  中,若
中,若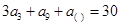 ,则
,则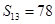 ”为真命题,由于印刷问题,括号处的数模糊不清,可算得括号内的数为 .
”为真命题,由于印刷问题,括号处的数模糊不清,可算得括号内的数为 .