题目内容
不等式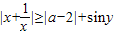 对一切非零实数x,y均成立,则实数a的范围为 .
对一切非零实数x,y均成立,则实数a的范围为 .
【答案】分析:由对勾函数的性质,我们可以求出不等式左边的最小值,再由三角函数的性质,我们可以求出siny的最大值,若不等式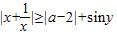 恒成立,则|a-2|≤1,解这个绝对值不等式,即可得到答案.
恒成立,则|a-2|≤1,解这个绝对值不等式,即可得到答案.
解答:解:∵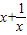 ∈(-∞,-2]∪[2,+∞)
∈(-∞,-2]∪[2,+∞)
∴|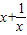 |∈[2,+∞),其最小值为2
|∈[2,+∞),其最小值为2
又∵siny的最大值为1
故不等式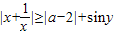 恒成立时,
恒成立时,
有|a-2|≤1
解得a∈[1,3]
故答案为[1,3]
点评:本题考查的知识点是绝对值三角不等式的解法,其中根据对勾函数及三角函数的性质,将不等式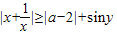 恒成立转化为|a-2|≤1,是解答本题的关键.
恒成立转化为|a-2|≤1,是解答本题的关键.
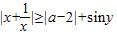 恒成立,则|a-2|≤1,解这个绝对值不等式,即可得到答案.
恒成立,则|a-2|≤1,解这个绝对值不等式,即可得到答案.解答:解:∵
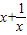 ∈(-∞,-2]∪[2,+∞)
∈(-∞,-2]∪[2,+∞)∴|
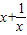 |∈[2,+∞),其最小值为2
|∈[2,+∞),其最小值为2又∵siny的最大值为1
故不等式
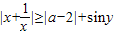 恒成立时,
恒成立时,有|a-2|≤1
解得a∈[1,3]
故答案为[1,3]
点评:本题考查的知识点是绝对值三角不等式的解法,其中根据对勾函数及三角函数的性质,将不等式
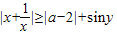 恒成立转化为|a-2|≤1,是解答本题的关键.
恒成立转化为|a-2|≤1,是解答本题的关键. 
练习册系列答案
相关题目
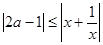 对一切非零实数
对一切非零实数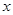 恒成立,则实数
恒成立,则实数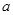 的取值范围是 .
的取值范围是 . 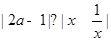 对一切非零实数
对一切非零实数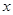 恒成立,则实数
恒成立,则实数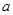 的
的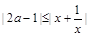 对一切非零实数
对一切非零实数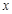 恒成立,则实数
恒成立,则实数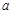 的取值范围是
的取值范围是 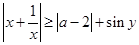 对一切非零实数
对一切非零实数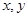 均成立,则实数
均成立,则实数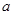 的范围为
的范围为
 对一切非零实数
对一切非零实数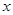 恒成立,则实数
恒成立,则实数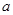 的取值范围
的取值范围