题目内容
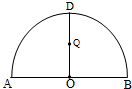 如图所示,为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
如图所示,为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)过D点且与AB不垂直的直线l与曲线C相交于不同的两点M、N,问是否存在这样的直线l使
| OM |
| ON |
| AQ |
分析:(Ⅰ)先以AB,OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系,利用曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变可得曲线C为以O为中心,以A,B为焦点的椭圆,再求出对应的a,b,c即可.
(Ⅱ)先把直线直线l的方程与椭圆方程联立,求出点M、N的坐标和斜率的关系以及斜率的取值范围,再利用
+
与
平行,求出对应的斜率看是否符合要求即可.
(Ⅱ)先把直线直线l的方程与椭圆方程联立,求出点M、N的坐标和斜率的关系以及斜率的取值范围,再利用
| OM |
| ON |
| AQ |
解答:解:(Ⅰ)以AB,OD所在直线分别为x轴、y轴,O为原点,建立平面直角坐标系.(1分)|PA|+|PB|=|QA|+|QB|=2
=2
>|AB|=4
∴曲线C为以O为中心,以A,B为焦点的椭圆,(3分)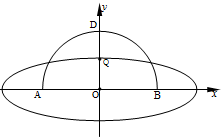
设长半轴长为a,短半轴长b,半焦距为c
∴a=
,c=2,b=1所以所求椭圆C的方程为
+y2=1(5分)
(Ⅱ)设存在这样的直线l使
+
与
平行,设直线l方程为y=kx+2
由
消去Y,整理得(5k2+1)x2+20kx+15=0,(7分)
设M(x1,y1),N(x2,y2)△=(20k)2-4(5k2+1)×15=20(5k2-3)>0?k2>
.
x1+x 2=
,y1+y2=k(x1+x2)+4=
(9分)
+
=(x1+x 2,y1+y2),
=(2,1)
∵
+
与
平行
∴
×1=
×2∴k=-
(11分)
∴k=-
与k2>
矛盾
所以不存在这样的直线l使
+
与
平行(12分)
| 22+1 |
| 5 |
∴曲线C为以O为中心,以A,B为焦点的椭圆,(3分)

设长半轴长为a,短半轴长b,半焦距为c
∴a=
| 5 |
| x2 |
| 5 |
(Ⅱ)设存在这样的直线l使
| OM |
| ON |
| AQ |
由
|
设M(x1,y1),N(x2,y2)△=(20k)2-4(5k2+1)×15=20(5k2-3)>0?k2>
| 3 |
| 5 |
x1+x 2=
| -20k |
| 5k2+1 |
| 4 |
| 5k2+1 |
| OM |
| ON |
| AQ |
∵
| OM |
| ON |
| AQ |
∴
| -20k |
| 5k2+1 |
| 4 |
| 5k2+1 |
| 2 |
| 5 |
∴k=-
| 2 |
| 5 |
| 3 |
| 5 |
所以不存在这样的直线l使
| OM |
| ON |
| AQ |
点评:本题涉及到圆,直线于椭圆以及向量共线问题,是对知识的综合考查.作这一类型题,一定要认真读题,把题中条件转化为数学符号.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
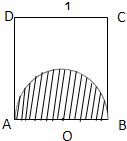 如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( )
如图所示,以边长为1的正方形ABCD的一边AB为直径在其内部作一半圆.若在正方形中任取一点P,则点P恰好取自半圆部分的概率为( ) (2012•湛江一模)一个几何体的三视图如图所示,正视图是正方形,俯视图为半圆,侧视图为矩形,则其表面积为( )
(2012•湛江一模)一个几何体的三视图如图所示,正视图是正方形,俯视图为半圆,侧视图为矩形,则其表面积为( )
 (2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
(2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论: