题目内容
9.若函数f(x)定义域为{1<x<2},则函数f(x2+1)的定义域为(-1,0)∪(0,1).分析 利用函数的定义域,直接求解新函数的定义域即可.
解答 解:函数f(x)定义域为{1<x<2},可得:1<x2+1<2,
解得x∈(-1,0)∪(0,1).
故答案为:(-1,0)∪(0,1).
点评 本题考查函数的定义域的求法,考查计算能力.

练习册系列答案
相关题目
5.已知f(x)在定义域(-4,1)上是减函数,且f(1+a)<f(3a-1),则a的取值范围是( )
| A. | (-∞,1) | B. | (-1,0) | C. | (-1,1) | D. | (0,1) |
1.集合A={a,b},其中非空真子集个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.已知函数y=f(x)的图象如图,那么f(x)的表达式为( )
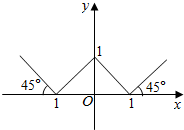

| A. | $\sqrt{{x}^{2}-2x+1}$ | B. | $\sqrt{{x}^{2}-2|x|+1}$ | C. | |x2-1| | D. | -2|x|+1 |