Question

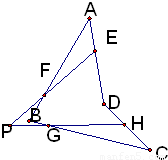
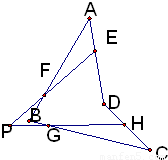
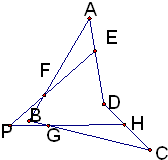在空间四边形各边AD、AB、BC、CD上分别取E、F、G、H四点，如果EF、GH交于一点P，则点P

1. A.
   一定在直线BD上
2. B.
   一定在直线AC上
3. C.
   在直线BD或AC上
4. D.
   不在直线AC上也不在直线BD上

Answer 1

A
分析：由已知中我们易得到EF在平面ABD内，GH在平面CBD内，平面ABD与平面CBD的交线为BD，若EF、GH交于一点P，则P点即在平面ABD内，又在平面CBD内，由公理3可得，P点一定在平面ABD和平面BCD的交线BD上，进而得到答案．
解答：若EF、GH交于一点P，
则E，F，G，H四点共面
又∵EF?平面ABD，GH?平面CBD，平面ABD∩平面CBD=BD，
∴P∈平面ABD，且P∈平面CBD，
由公理3可得
P∈BD
故选A
点评：本题考查的知识点是平面的基本性质及推论，其中熟练掌握平面的性质的几个公理及其适用范围，是解答本题的关键．