题目内容
化简
（x∈R，k∈Z）的结果为 ．
【答案】分析：把原式利用和差化积公式cosα+cosβ=2cos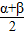
cos
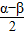化简，合并后再利用诱导公式cos（2kπ+α）=cosα及特殊角的三角函数值计算后即可得到最后结果．
解答：解：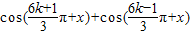
=2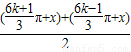cos
cos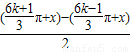
=2cos（2kπ+x）cos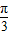
=2×
cosx
=cosx．
故答案为：cosx
点评：此题考查了三角函数的和差化积公式，诱导公式及特殊角的三角函数值，熟练掌握公式是解本题的关键．
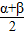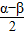cos化简，合并后再利用诱导公式cos（2kπ+α）=cosα及特殊角的三角函数值计算后即可得到最后结果．解答：解：
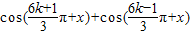
=2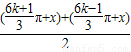cos
cos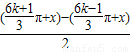=2cos（2kπ+x）cos
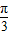
=2×
cosx=cosx．
故答案为：cosx
点评：此题考查了三角函数的和差化积公式，诱导公式及特殊角的三角函数值，熟练掌握公式是解本题的关键．
练习册系列答案
相关题目
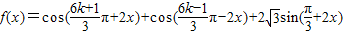（x∈R，k∈Z）并求函数f（x）的值域和最小正周期．
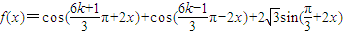（x∈R，k∈Z）并求函数f（x）的值域和最小正周期．
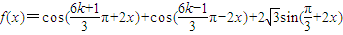（x∈R，k∈Z）并求函数f（x）的值域和最小正周期．
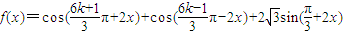（x∈R，k∈Z）并求函数f（x）的值域和最小正周期．